Сергей Львовский

В популярных статьях о математиках XX века рассказать об их научных достижениях обычно невозможно, приходится отделываться общими словами. Герой этой статьи составляет исключение: об одной из его теорем мы кое-что расскажем

Макс Ден (1878–1952). Фото: Konrad Jacobs, Oberwolfach Photo Collection

Карьера в Германии

Макс Вильгельм Ден родился в Гамбурге в 1878 году в семье врача. Окончив гимназию, он поступил во Фрайбургский университет, но затем перевёлся в университет города Гёттингена — в то время ведущий математический центр мира. В Гёттингене научным руководителем Дена стал великий математик Давид Гильберт. Под его руководством Ден защитил диссертацию о неевклидовых геометриях. Вскоре после этого Ден сделал ту самую работу, о которой мы расскажем подробнее, а затем занялся топологией — новым в то время разделом математики — и получил в этой науке много важных результатов. Он продолжал заниматься математикой в Германии даже после того, как нацисты уволили его из университета за еврейское происхождение, и в 1938 году опубликовал (за границей — в Швеции) одну из основополагающих топологических работ. Да и самая последняя статья Дена, вышедшая в 1950 году, когда он уже жил в Америке, также посвящена его любимой маломерной топологии.

Третья проблема Гильберта

Давид Гильберт (1862–1943), немецкий математик-универсал

В августе 1900 года в Париже на Втором международном математическом конгрессе Гильберт сформулировал список из 23 задач, решение которых, по его мнению, особенно важно для развития математики в наступающем XX веке. Десятка полтора из этих проблем сейчас решены; первой поддалась «третья проблема», и решил её именно Макс Ден.

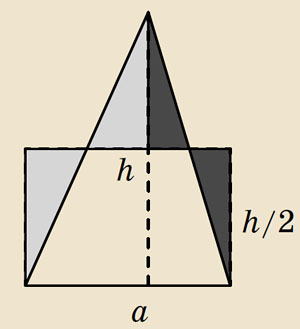
Рис. 1

Чтобы понять, в чём эта проблема заключалась, вспомним, что площадь треугольника равна половине произведения основания на высоту. Доказать это можно «методом разрезания и складывания»: например, остроугольный треугольник с основанием a и высотой h разрезается на части, из которых складывается прямоугольник с основанием a и высотой h/2 (рис. 1). Как говорят, остроугольный треугольник с основанием a и высотой h и прямоугольник со сторонами a и h/2 равносоставлены: один из них можно разрезать на части, из которых можно сложить другой.

Имеется аналогичное утверждение и для объёмов: объём пирамиды равен одной трети произведения площади её основания на высоту. Но ни в одном учебнике не рассказывается, на какие части надо разрезать пирамиду с площадью основания P и высотой h, чтобы потом сложить из них параллелепипед или призму с площадью основания P и высотой h/3 — формулы для объёма пирамиды доказываются совсем иначе.

Вот, например, как это сделано в классическом школьном учебнике геометрии А. П. Киселёва.

Для простоты найдём объём треугольной пирамиды SABC, у которой ребро SB перпендикулярно основанию ABC (у Киселёва рассмотрен и общий случай). Пусть площадь основания — треугольника ABC  — равна P, а длина ребра SB — высоты пирамиды — равна h. Достроим нашу пирамиду до призмы ABCESD с площадью основания P и высотой h (рис. 2). Эта призма разбивается на три треугольные пирамиды: нашу исходную SABC, плюс ещё пирамиды CDES и CAES. Если удастся доказать, что объёмы этих трёх пирамид равны, мы получим, что объём пирамиды SABC равен трети объёма призмы ABCESD, то есть Ph/3. Но как установить равенство этих трёх объёмов, ведь три пирамиды, на которые разбита призма ABCESD, не обязательно будут равными фигурами? Это делается с помощью следующей леммы.

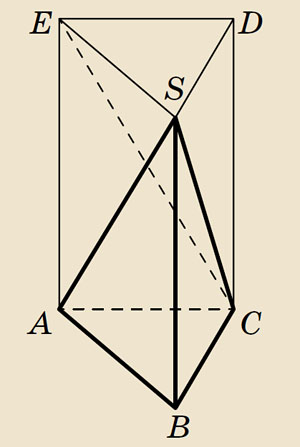
Рис. 2

Лемма. Если у двух пирамид равны и площади оснований, и высоты, то и объёмы этих пирамид равны.

Из леммы искомое равенство объёмов выводится легко. В самом деле, объёмы пирамид SABC и CDES  равны, потому что у них совпадают и площади оснований (треугольников ABC и DSE), и длины высот (отрезков SB и CD), а у пирамид CDES и CAES объёмы тоже равны: если рассмотреть их как треугольные пирамиды с вершиной S, то высота у них будет общей, а основания (треугольники CDE и EAC) имеют, очевидно, равную площадь.

Остаётся, стало быть, доказать лемму — но тут и начинаются настоящие трудности! Сделать из одной пирамиды другую с помощью разрезания и складывания у авторов учебников никак не получалось, так что приходилось проводить рассуждения, выходящие за рамки «чистой геометрии» и использующие такое математическое понятие, как предел.

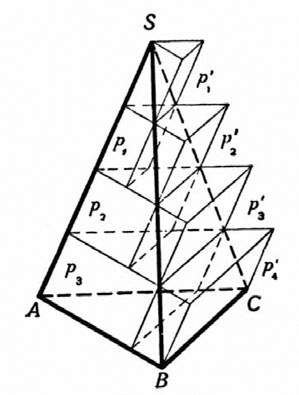
Чертёж к традиционному доказательству леммы: обе пирамиды приближают (изнутри и снаружи) объединениями треугольных призм, а затем переходят к пределу при высотах призм, стремящихся к нулю

Когда Давид Гильберт в самом конце XIX века занялся вопросами логического построения геометрии, он в числе прочего поставил вопрос, насколько можно в геометрии обойтись без таких «негеометрических» рассуждений. Ему это удалось при построении теории площадей многоугольников, но с объёмами многогранников ничего не получалось; в результате у Гильберта (как полувеком ранее у другого великого математика, К. Ф. Гаусса) возникло подозрение, что «чисто геометрическое» построение стереометрии и вовсе невозможно. Свою третью проблему Гильберт формулирует так.

Существуют ли такие две треугольные пирамиды с равными высотами и одинаковой площадью основания, что первую из них невозможно разбить на конечное число многогранников, из которых можно сложить вторую?

Мы бы сегодня сказали: если есть две пирамиды, одинаковые по площади основания и по высоте, могут ли они быть неравносоставленными? Иными словами: можно ли доказать с помощью разрезаний и складываний нашу лемму?

На самом деле Гильберт хотел большего: он предлагал найти пример двух пирамид с одинаковыми площадями оснований и высотами, которые не только не были бы равносоставленными, но не были бы ещё и «равнодополняемыми». Два многогранника называются равнодополняемыми, если к каждому из них можно добавить конечное число одних и тех же многогранников (поворачивая их как угодно) так, чтобы получающиеся большие многогранники стали равносоставленными. Ясно, что объёмы равнодополняемых фигур совпадают, и если бы две пирамиды, о которых идёт речь в лемме, оказались равнодополняемыми, мы получили бы её чисто геометрическое доказательство.

Русский перевод книги Гильберта, в которой он изложил свои исследования по аксиоматическому построению геометрии. С этими исследованиями связаны и тема диссертации Дена, и его статьи о равносоставленности многогранников

Что сделал Ден

Доклад Гильберта с перечнем проблем был опубликован в третьем номере «Докладов Гёттингенского королевского научного общества» за 1900 год. И в тот же самый номер этого журнала вошла статья Дена «О равносоставленных многогранниках», в которой приводился пример двух неравносоставленных треугольных пирамид с одинаковыми площадью основания и высотой. Решение проблемы увидело свет одновременно с её формулировкой!

Впрочем, оставалась ещё возможность, что пирамиды, неравносоставленность которых установил Ден, всё же равнодополняемы. Однако в следующем 1901 году Ден доказал, что существуют треугольные пирамиды с равными площадями оснований и высотами, не являющиеся ни равносоставленными, ни равнодополняемыми. Вот теперь можно было точно сказать, что третья проблема Гильберта решена, а чисто геометрически вывести формулу для объёма пирамиды невозможно! Кстати, в учебнике Киселёва (в издании 1914 года) упоминаются работы Дена и говорится, какое отношение они имеют к преподаванию геометрии.

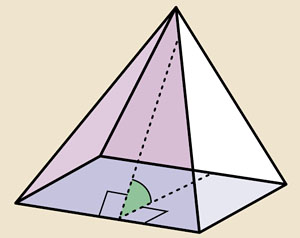
Двугранный угол — угол между гранями

Скажем о результатах Дена чуть подробнее. В работе 1900 года он доказывает вот что. Пусть P и Q — два многогранника. Если у многогранника P всего n рёбер, обозначим величины двугранных углов при этих рёбрах через α₁, α₂, ... , α_n. Аналогично, величины двугранных углов при рёбрах многогранника Q  обозначим через β₁, β₂, ... , β_m.

Необходимое условие равносоставленности. Если в этих условиях многогранники P и Q равносоставлены, то найдутся такие натуральные числа p₁, p₂, ... , p_n и q₁, q₂, ... , q_m, что суммы p₁α₁ + p₂α₂ +...+ p_nα_n и q₁β₁ + q₂β₂ + ... + q_mβ_m различаются на рациональное число градусов.

Книга «Математический дивертисмент» (МЦНМО, 2016)

Вот как из этого условия можно вывести, что правильный тетраэдр неравносоставлен ни с каким прямоугольным параллелепипедом. Все двугранные углы при двенадцати рёбрах прямоугольного параллелепипеда — прямые, так что при любых натуральных числах q₁, q₂, ..., q₁₂ сумма q₁β₁ + q₂β₂ + ... + q₁₂β₁₂ кратна 90° и тем самым выражается рациональным (и даже целым) числом градусов. С другой стороны, двугранные углы при всех шести рёбрах правильного тетраэдра равны одному и тому же углу (обозначим его α), так что сумма p₁α₁ + p₂α₂ + ... + p₆α₆ равна kα для некоторого натурального k. Значит, если правильный тетраэдр и параллелепипед равносоставлены, то угол kα, а значит и угол α, выражается рациональным числом градусов. Можно проверить, что для данного угла α это не так, и получаем противоречие.

Формулировку и доказательство результата Дена 1901 года можно посмотреть в книге С. Л. Табачникова и Д. Б. Фукса «Математический дивертисмент» (лекция 22).

Под конец жизни

Страница из работы Р. Брикара 1896 года с почти той же формулировкой необходимого условия равносоставленности, которая появится в статье Дена 1900 года. Вместо доказательства своего утверждения Брикар ограничивается словами «легко видеть, что». Вероятно, в опущенном Брикаром доказательстве имелась ошибка

Большинству математиков, имевших несчастье в 30-е годы прошедшего века оказаться в Центральной Европе и вообще на территории, оккупированной Германией в ходе Второй мировой войны, прожить спокойную жизнь не довелось: кто не успел вовремя эмигрировать, тот погиб или, в лучшем случае, пережил очень тяжёлое время. Георг Пик¹, Отто Блюменталь и Альфред Таубер погибли в нацистских концлагерях, куда они были заключены просто за своё еврейское происхождение. Фридриха Хартогса и Феликса Хаусдорфа нацистские преследования (за ту же «вину») довели до самоубийства. Юлиуш Шаудер и Станислав Сакс были казнены за участие в польском антинацистском сопротивлении. Гуго Штейнгауз с 1941 по 1945 год был вынужден скрываться под чужим именем. Стефан Банах в годы немецкой оккупации вместо работы по специальности стал объектом бесчеловечных медицинских экспериментов...

¹ См. статью Г. Мерзона «Площади многоугольников и тающий лёд» о формуле Пика в «Квантике» № 9 за 2018 год.

Дену повезло больше: он успел уехать в последний момент перед тем, как началось самое страшное. В начале 1939 года он переехал из Германии в Норвегию, нашёл там работу, а когда Норвегию оккупировали нацисты, уехал в США, для чего ему пришлось проехать больше чем полмира: сначала пересечь СССР по Транссибирской магистрали, затем из Владивостока по морю перебраться в Японию и, наконец, из Японии на корабле через Тихий океан — в США.

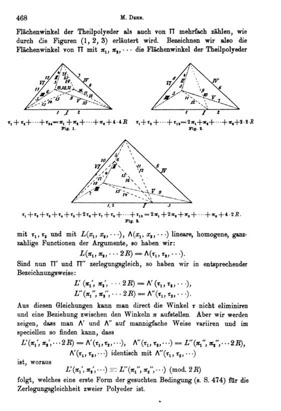
Страница из работы Дена

На свою новую родину Макс Ден с супругой прибыли в самом начале 1941 года. Первые годы ему жилось непросто: приходилось за маленькую зарплату учить слабых студентов то в одном, то в другом университете низкого уровня. Но в 1945 году Дену улыбнулась удача: его приняли на работу в Блэк-Маунтин-колледж в штате Северная Каролина. Это было очень своеобразное учебное заведение, основанное в 1933 году как независимый университет, похожий по устройству на коммуну. Все управленческие решения в колледже принимались на общем собрании студентов и преподавателей. Студенты и преподаватели постоянно жили на кампусе среди леса; они питались в общих столовых, а еда для этих столовых выращивалась на университетской ферме, где полевыми работами занимались (наряду с учёбой и преподаванием) опять-таки преподаватели и студенты.

У Блэк-Маунтин-колледжа не было аккредитации (так что он не выдавал официальных дипломов), ему вечно не хватало средств, и Дену платили очень мало, но он, похоже, был на этой работе счастлив. Ден преподавал студентам не только математику, но ещё философию, латынь и греческий, ходил с ними в походы, занимался, как сейчас бы сказали, экологией (боролся против вырубки окрестных лесов)... В 1952 году Макс Ден вышел на пенсию. Предполагалось, что он продолжит жить на кампусе и будет исполнять обязанности консультанта, но уже в следующем месяце он умер от сердечного приступа. Похоронили Дена в том же лесу, в котором был расположен университетский кампус.

Кампус Блэк-Маунтин-колледжа

Имя Макса Дена осталось в науке: по сей день в топологии важную роль играют «скручивание Дена» и «хирургия Дена».

elementy.ru