ТЕТРАФЛЕКСАГОНЫ

Об изобретении гексафлексагонов и их построении подробно говорится в главе 1. В тесном родстве с гексафлексагонами находится множество игрушек, имеющих форму четырехугольника. Они известны под общим названием тетрафлексагонов. И если свойства гексафлексагонов были тщательно исследованы (по существу, была построена полная математическая теория гексафлексагонов), то о тетрафлексагонах известно гораздо меньше. Артур X. Стоун и его друзья (в особенности Джон У. Тьюки) посвятили много времени складыванию и анализу этих четырехсторонних разновидностей флексагонов, но им так и не удалось построить всеобъемлющую теорию, которая охватывала бы все на первый взгляд ничем не связанные между собой разновидности этих головоломок. Тем не менее некоторые из тетрафлексагонов представляют особый интерес с точки зрения занимательной математики.

Рассмотрим сначала простейший тетрафлексагон. Он имеет три поверхности и поэтому называется тритетрафлексагоном. Его легко сложить из полоски бумаги, изображенной на рис. 97 (а — лицевая, б — оборотная сторона полоски). Перенумеруем квадраты на обеих сторонах полоски так, как это сделано на рис. 97.

Перевернув полоску бумаги оборотной стороной вверх, перегнем ее слева направо вдоль вертикали, разделяющей две тройки, а затем загнем самый правый нижний квадрат (рис. 97, в) и склеим его оборотную сторону с верхним квадратом прозрачной лентой (рис. 97, г).

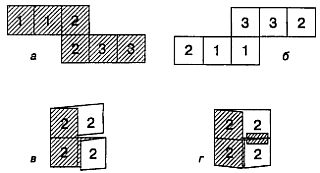
Рис. 97 Как сделать тритетрафлексагон.

На верхней поверхности окажутся квадраты с двойками, на нижней — квадраты с единицами. Перегнем тритетрафлексагон по вертикальной оси и сложим его вдвое так, чтобы квадраты с двойниками оказались снаружи. Вывернув получившуюся «книжечку» спереди, мы увидим, что квадраты с единицами исчезли, спрятались внутрь, зато стали видны квадраты с тройками.

Честь изобретения этого устройства принадлежит не Стоуну и его друзьям — вот уже несколько столетий по этой схеме делают шарнирные соединения «двойного действия». На моем письменном столе, например, стоят две рамочки для фотографий, которые соединены так, что образуют тритетрафлексагон, с одинаковой легкостью открывающийся в обе стороны.

Ту же конструкцию можно обнаружить и во многих детских игрушках. Наиболее известны цепочки из деревянных брусков или пластмассовых кубиков, скрепленных между собой крест-накрест проволочками или тесемками. Стоит лишь определенным образом передвинуть отдельные звенья цепочки, как создается полное впечатление, что верхний кубик перемещается в самый низ цепи. На самом деле это не более чем обман зрения, вызванный последовательным изгибанием шарнирных соединений, выполненных по схеме тритетрафлексагона. В 90-е годы прошлого столетия в США широкой популярностью пользовалась основанная на этом же принципе игрушка под названием «Лестница Якова» (рисунок и описание этой игрушки можно найти в книге Альберта А. Гопкинса[33]). В наше время в магазинах игрушек можно было встретить ее современные варианты — «Кубики клик-клак» и «Кубики флип-флоп».

Существует по крайней мере шесть типов четырехсторонних трафлексагонов, известных под названием тетратетрафлексагоны.

Для изготовления их удобнее всего взять прямоугольный кусок тонкого картона и разграфить его на 12 квадратов. Нумерация квадратов на обеих сторонах листа показана на рис. 98 (а и б).

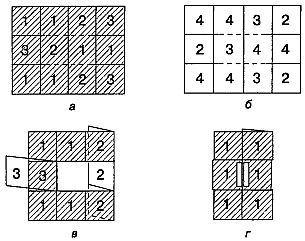
Рис. 98 Как сделать тетратетрафлексагон.

Пунктиром обозначены линии разрезов. Взяв прямоугольник так, чтобы лицевая его сторона (рис. 98, а) была обращена к нам, отогнем вниз и налево язычок из двух центральных квадратов с цифрами 2 и 1 и подогнем правый столбец. То, что при этом получится, показано на рис. 98, в. Еще раз подогнем правый столбец и загнем на себя и вправо квадрат с тройкой, торчавший до сих пор слева. После этих операций все квадраты с 1 окажутся сверху. Два центральных квадрата склеим прозрачной лентой так, как показано на рис. 98, г.

Вы без труда догадаетесь, как следует перегнуть тетратетрафлексагон, чтобы увидеть квадраты с единицами, двойками и тройками. Несколько труднее увидеть четверки. Разумеется, рвать картон не разрешается. Более сложные тетрафлексагоны этого типа с четным числом поверхностей можно построить из аналогичных прямоугольников, а тетрафлексагоны с нечетным числом «листов» — из зигзагообразных полосок, похожих на ту, из которой мы сложили тритетрафлексагон. В самом деле, чтобы построить трафлексагон этого типа, достаточно взять два ряда квадратиков, но добавление одного или нескольких лишних рядов без изменения основной структуры намного облегчает работу с моделью.

Тетратетрафлексагон, изображенный на рис. 98, часто используется для рекламных трюков: трудность отыскания «листка» с четверками превращает его в занимательную головоломку. Много таких складных игрушек мне доводилось видеть еще в тридцатые годы. В одной из них к скрытому развороту флексагона была приклеена «счастливая» монетка, которую нужно было найти. В другой, которая называлась «Cherchez la femme»,[34] задача заключалась в том, чтобы отыскать портрет молодой девушки. И сейчас в магазинах можно увидеть старинный детский фокус, обычно известный под названием «Волшебный доллар». Шарнирные соединения этой игрушки, выполненные по схеме тритетрафлексагона, позволяют показывать незамысловатые фокусы с исчезновением долларовой купюры и других плоских предметов.

Существует совсем другая разновидность тетрафлексагонов, обладающих необычным свойством: их можно сгибать вдоль двух взаимно перпендикулярных осей. Они также имеют по четыре и больше разворотов. На рис. 99 показано, как построить одну из фигур этого типа — гексатетрафлексагон. Прежде всего нужно взять полоску бумаги, вырезанную в форме квадратной рамки (рис. 99, а — вид спереди, б — вид сзади), разграфить ее на квадраты и перенумеровать их так, как показано на рисунке.

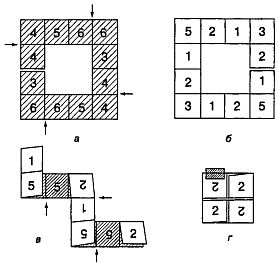
Рис. 99 Как сделать гексатетрафлексагон.

После этого полоску бумаги нужно перегнуть вдоль всех прямых, которые отделяют друг от друга соседние квадраты. Линии сгиба должны быть «долинами», а не «горными хребтами», то есть сгибы должны быть обращены острием вниз. Наметив все линии сгиба, полоску нужно разгладить и затем снова сложить, перегнув ее вдоль прямых, указанных на рис. 99, а стрелками (направление сгиба нужно выбирать так, чтобы не «переутюживать» в противоположную сторону уже сделанные складки). Тогда обратная сторона полоски примет вид, показанный на рис. 99, в. Перегнем ее еще раз вдоль линий, указанных на рис. 99, в стрелками, и заправим квадрат с цифрой 3 под квадрат с цифрой 2. В результате все четыре верхних квадрата окажутся помеченными цифрами 2 (рис. 99, г). К левому верхнему квадрату с цифрой 2 приклеим прозрачную ленту, а другой конец ленты приклеим к квадрату с 1, находящемуся с обратной стороны флексагона.

Гексатетрафлексагон можно перегибать и по вертикальной, и по горизонтальной осям. Если брать полоски бумаги в форме квадратных рамок больших размеров, то будут получаться флексагоны с числом разворотов, увеличивающимся на 4: 10, 14, 18, 22 и т. д.

Для получения тетрафлексагонов других порядков следует брать полоски бумаги иной формы.

Самую замечательную головоломку — флексотрубку — Стоун случайно открыл, работая над флексагонами, имеющими форму прямоугольного треугольника («Для них, — сообщал он в одном письме, — мы не стали придумывать специального названия из соображений человеколюбия»). Построив плоский флексагон в форме квадрата, Стоун к своему изумлению обнаружил, что может превратить его в трубку. Как показали дальнейшие эксперименты, трубку можно полностью вывернуть наизнанку, если воспользоваться сложной системой сгибов по сторонам прямоугольных треугольников.

Флексотрубка делается из полоски бумаги, поделенной на четыре квадрата (рис. 100, а), каждый из которых в свою очередь разделен на четыре прямоугольных треугольника.

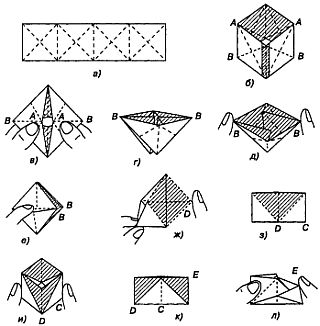
Рис. 100 Как сложить и вывернуть флексотрубку.

Перегнув полоску в обе стороны по сторонам и диагоналям квадратов, склеим ее концы. У нас получится трубка квадратного сечения. Задача заключается в том, чтобы, пользуясь только намеченными сгибами, вывернуть эту трубку наизнанку. Более долговечную модель можно сделать, наклеив на матерчатую ленту 16 треугольников из картона или тонкого металла. Между треугольниками нужно оставить небольшой зазор, чтобы трубка сгибалась. Выкрасив эти треугольники с одной стороны, вы всегда сможете видеть, как далеко вам удалось продвинуться в выворачивании трубки.

Один из способов решения этой отнюдь не простой задачи показан на рис. 100, б— л. Совместив точки А, превратим трубку в плоский квадрат (рис. 100, в). Положив квадрат на стол, перегнем его вдоль прямой ВВ так, чтобы верхняя половина накрыла нижнюю. У нас получится треугольник, изображенный на рис. 100, г.

Нажав на вершины В, сведем их вместе так, чтобы треугольник превратился в маленький квадрат (рис. 100, д). Особенно внимательно при этом нужно следить за тем, чтобы внутренние выступы разошлись в противоположные стороны. Распечатаем квадрат (рис. 100, е): потянув за середину кармашка С, опустим ее до отказа вниз. Наша бумажная лента будет после этого сложена так, как показано на рис. 100, ж. Треугольник с вершиной в точке D подогнем внутрь, чтобы получился прямоугольник (рис. 100, з).

Раскрыв его, мы снова увидим трубку квадратного сечения (рис. 100, и), которая оказывается вдвое короче исходной.

Проделана половина всех операций — вывернута ровно половина трубки. Сплющим трубку еще раз, снова превратив ее в прямоугольник (рис. 100, к). Этот прямоугольник отличается от показанного на рис. 100, з тем, что он получается при сплющивании трубки по другой диагонали. Начав с операции, показанной на рис. 100, л, «уничтожим следы» того, что уже было сделано, то есть будем производить все действия в обратном порядке. В результате мы и получим вывернутую наизнанку трубку. Известны еще по крайней мере два совершенно различных, но столь же хитроумных способа выворачивания флексотрубки. Додуматься до каждого из них так же трудно, как и до способа, о котором мы только что рассказали.

Не так давно Стоун сумел доказать, что склеенную в форме цилиндра ленту любой ширины всегда можно вывернуть наизнанку, перегибая ее вдоль конечного числа прямых, однако общий метод слишком сложен для того, чтобы мы могли объяснить его здесь.

Естественно, возникает вопрос: можно ли вывернуть бумажный пакет (то есть трубку прямоугольного сечения, заклеенную с одного конца) за конечное число перегибаний? Эта задача еще не решена.

По-видимому, ответ будет отрицательным независимо от соотношения размеров пакета, хотя найти удовлетворительное доказательство этого факта, по всей вероятности, будет крайне трудно.

Взяла с

    

Как сделать флексагон

 

  


Центрально-симметричные, плоские фигуры. Чаще всего сборные, состоящие из нескольких модулей.


Авторы: Нина Острун, Алексей Киселев





Авторы: Нина Острун, Алексей Киселев







Авторы: Нина Острун, Алексей Киселев







Авторы: Нина Острун, Алексей Киселев







Автор: Виктор Лащенко







Автор: Виктор Лащенко
Эта несложная фигура складывается из восьми квадратов одинакового размера. Удачным может быть использование двух контрастных цветов.






=============================================================


Симметричные, объемные фигуры. Чаще всего сборные, состоящие из нескольких модулей.



Автор: Нина Острун








Автор: Виктор Лащенко








=================================


И утки, и журавли, и колибри... И даже те, кого в природе не существует. Главное, чтобы был клюв, крылья и хвост.

Автор: Мария Лащенко







Автор: Мария Лащенко









Автор: Роман Свиридов




На 7-ом этапе
Вам придется практически полностью развернуть фигуру и затем сложить ее
опять, но с учетом показанных сгибов. То же самое придется сделать на 14-ом этапе, складывая голову Орла.


Автор: Мария Лащенко






Автор: Дмитрий Шомин







Автор: Дмитрий Шомин


Фигура складывается из треугольного листа бумаги, причем чем меньше
исходный треугольник, тем больше бумажная Колибри похожа на настоящую.







Автор: Уля Лащенко

При складывании фигуры применяется оригинальная складка, за счет которой Курица становится объемной и может "высиживать" яйцо.




========================================================



Сделайте свой бумажный зоопарк! Будьте осторожны - не все звери безобидны.

Автор: Вонг Сэн
Гонконг




Схема предоставлена для публикации "Музеем Оригами". Схема нарисована автором.


Автор: Дэйв Брилл
Великобритания





Схема предоставлена для публикации "Музеем Оригами". Схема нарисована автором.


Автор: Роман Свиридов



На 12 этапе получается Лиса. Если двигать нижние углы, так как показано на диаграмме, Лиса начинает "разговаривать". На 15 этапе получается Осел. Естественно, он умеет делать все то же, что и Лиса.


Автор: Павел Борисов






Автор: Роман Свиридов

Мышка - животное маленькое, поэтому и квадрат для фигуры лучше использовать маленький.




Длиный хвост можно согнуть различными способами и, за счет этого, сложить несколько разных мышек.



Автор: Роман Свиридов



На 11-ом этапе, отгибая Лисе хвост, держите фигуру за точки, помеченные белыми кружками.



Автор: Павел Борисов

Очень симпатичный Ежик. Правда некоторые считают его маленьким Дикобразом.







Автор: Уля Лащенко





=====================================================


Фигуры, которые не попали ни в один из предыдущих разделов.



Автор: Мария Лащенко








Автор: Виктор Лащенко


Вариант простого плоского флексагона, интереснейшей динамической фигуры
из "головоломной" математики, сложенный из трех квадратов.














Автор: Светлана Опаричева





Подготовка квадратов




Бумагу для элементов Розы лучше выбрать одинакового цвета с обеих
сторон. Разный цвет сторон бумаги показан для лучшей читаемости схемы.
Вам понадобяться три квадрата (I, II и III).


Для внешнего элемента Роза используйте квадрат I. Начиная с 13-го этапа, элемент Розы становиться трехмерным и остальные этапы проделываются "на весу".

Внутренний элемент
Внутренние элементы складываются из квадратов II и III. Для каждого из них, схема складывания повторяет этапы 1-12
предыдущей схемы. Если Вы хотите сложить упрощенный варианта Розы, Вы
можете использовать только один внутренний элемент, для которого
используйте квадрат II. Квадрат III в этом случае Вам не понадобиться.

Этап 1. У всех частей Розы пригибаем внутреннее ребро к боковой поверхности (на диаграмме показан вид сверху). У I части отгибаем уголки немного наружу.
Этап 2.
Вкладываем получившиеся части одна в другую и немного закручиваем
"лепестки" Розы. После вставки одного модуля в другой, поверните
внутренний на 45 градусов и немного поднимите его уголки так, чтобы они
вошли в соответствующие внутренние углы внешнего модуля.



Автор: Роман Свиридов

Квадрат для складывания Бейсболки можно вырезать из разворота большой газеты.



Размер A равен половине размера головного убора. Пропорции козырька можно менять за счет изменения угла наклона сгибов на 7-ом этапе.



Автор: Мария Лащенко






Автор: Виктор Лащенко










Автор: Павел Борисов







Автор: Виктор Лащенко






Мозаику можно наращиваеть вверх, вниз, вправо и влево. На основе
соединения можно создавать не только различные плоские мозаичные
рисунки, но и объемные фигуры.


Автор: Виктор Лащенко

Рамку можно сделать для любой прямоугольной фотографии или открытки, был бы только лист бумаги подходящего размера.







Размеры исходного листа бумаги определяютьс размерами фотографии или
открытки, для которой складывается Рамка, выбраной произвольно толщиной
канта (X) и соотношениями, указанными на первом рисунке схемы.



Автор: Павел Борисов

Довольно убедительное попадание.







Автор: Виктор Лащенко

Сложенный из плотной бумаги Ковчег может уплыть довольно далеко.








Автор: Мария Лащенко



На этапе 10 получается форма (она изображена отдельно на вставке A),
которую можно использовать для дальнейших экспериментов и проб, из
которой можно получить несколько различных конечных форм насекомых. В
частности, можно создавать жуков различных пропорций, используя формы с
различными расстояниями S.


Этапы 1 - 8 - такие же, как и в 1-ой схеме. Также как и при складывании 1-го жука, здесь тоже, но только на 12-ом этапе, получается форма, изображенная на вставке B, которую также можно использовать для дальнейших экспериментов и проб.

Все фото и описания из этого и двух первых постов взяты с www.origami.ru

  

Флексагон - игрушка трансформер за 5 минут МК

Автор-BelMary

 

1.