-Рубрики
- Методические статьи (44)
- Развивающее обучение (16)
- Арифметика (7)
- Алгебра (4)
- Задачи на клетчатой бумаге (4)
- Проценты (2)
- Тригонометрия (1)
- Мои инструменты (29)
- Kandidat CMS (4)
- Интернет (4)
- Skype (3)
- Online доски (2)
- Youtube (2)
- Электронная почта (2)
- Фотошоп (2)
- Решения тестов ЕНТ (14)
- Уроки решения тестов ЕНТ (5)
- Курс HTML5 и CSS3. II. Программы и настройки (4)
- Курс HTML5 и CSS3. I. Введение (4)
- Верстка сайта (4)
- Бытовые наблюдения (3)
- Функциональные уравнения (3)
- Мои Интернет-проекты (3)
- Рецензии (3)
- Теория вероятностей (2)
- Задания типа В10 (2)
- Метод координат в задачах ЕГЭ (2)
- Комбинаторика (1)
- PHP (1)
- КУРС HTML5 И CSS3. III. ТЕКСТ (0)
- Решения задач (30)
- Решения тестов ЕГЭ (31)
- Задание типа В3 (2)
- Старые записи о Интернет-проектах (4)
-Метки
-Поиск по дневнику
-Подписка по e-mail
-Статистика
Выбрана рубрика Развивающее обучение.
Соседние рубрики: Тригонометрия(1), Проценты(2), Задачи на клетчатой бумаге(4), Арифметика(7), Алгебра(4)
Другие рубрики в этом дневнике: Функциональные уравнения(3), Теория вероятностей(2), Старые записи о Интернет-проектах(4), Решения тестов ЕНТ(14), Решения тестов ЕГЭ(31), Решения задач(30), Рецензии(3), Мои Интернет-проекты(3), Мои инструменты(29), Методические статьи(44), Метод координат в задачах ЕГЭ(2), КУРС HTML5 И CSS3. III. ТЕКСТ(0), Курс HTML5 и CSS3. II. Программы и настройки(4), Курс HTML5 и CSS3. I. Введение(4), Комбинаторика(1), Верстка сайта(4), Бытовые наблюдения(3), PHP(1)
Соседние рубрики: Тригонометрия(1), Проценты(2), Задачи на клетчатой бумаге(4), Арифметика(7), Алгебра(4)
Другие рубрики в этом дневнике: Функциональные уравнения(3), Теория вероятностей(2), Старые записи о Интернет-проектах(4), Решения тестов ЕНТ(14), Решения тестов ЕГЭ(31), Решения задач(30), Рецензии(3), Мои Интернет-проекты(3), Мои инструменты(29), Методические статьи(44), Метод координат в задачах ЕГЭ(2), КУРС HTML5 И CSS3. III. ТЕКСТ(0), Курс HTML5 и CSS3. II. Программы и настройки(4), Курс HTML5 и CSS3. I. Введение(4), Комбинаторика(1), Верстка сайта(4), Бытовые наблюдения(3), PHP(1)
Неравенства с радикалами |
Дневник |
В этой заметке мы рассмотрим решение одного типа иррациональных неравенств с радикалами. Если быть точнее рассмотрим известные мне решения неравенства типа 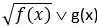 , где f(x) и g(x) - многочлены не выше второй степени.
, где f(x) и g(x) - многочлены не выше второй степени.
В качестве примера рассмотрим неравенство, заимствованное из книги И. И. Мельникова, И. Н. Сергеева "Как решать задачи по математике на вступительных экзаменах" (стр. 89). Скачать эту книгу можно отсюда: https://yadi.sk/d/G1wJWAxFeNqgG.
Решите неравенство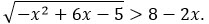
Решение I. Найдем сначала ОДЗ данного неравенства, то есть решим неравенство -х2 + 6х - 5 ≥ 0.
Для этого найдем корни квадратного трехчлена -х2 + 6х - 5. Эти корни мы получим после решения уравнения
-х2 + 6х - 5 = 0,
х2 - 6х + 5 = 0,
D = 36 - 20 = 16 = 42,
x1 = (6 + 4)/2 = 5,
x2 = (6 - 4)/2 = 1,
-(x - 5)(x - 1)≥ 0,
(x - 5)(x - 1)≤ 0.
Решением последнего неравенства будет отрезок [1; 5].
Возводить заданное неравенство в квадрат можно только в случае, когда правая и левая ее части неотрицательны. Поэтому на найденном ОДЗ приходится разбирать два случая.
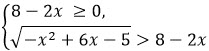 и
и 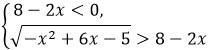
Рассмотрим первый случай, включая туда и ОДЗ.
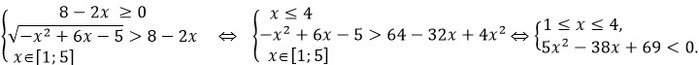
Решим неравенство 5x2 – 38x + 69 < 0.
5x2 – 38x + 69 = 0, D = 1444 – 1380 = 64,
x = (38 ± 8)/10, x1 = 3, x2 = 4,6;
5(x - 3)(x – 4,6) < 0,
Так как х ≤ 4, то x – 4,6 < 0 и х – 3 > 0, x > 3. Поэтому х ∈ (3; 4].
теперь второй случай также включая в него ОДЗ.
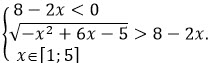
При 8 - 2х < 0 неравенство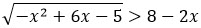 будет выполняться при всех х из ОДЗ. Поэтому будем иметь
будет выполняться при всех х из ОДЗ. Поэтому будем иметь
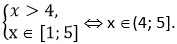
(3; 4] U (4; 5] =(3; 5].
Ответ: (3; 5].
Вот такое решение, конечно по стилю, приводится в указанном выше пособии.
Сейчас я покажу другое решение этого же неравенства.
Решение II.
Не повторяясь отмечу, что ОДЗ данного неравенства - отрезок [1; 5].
Вместо данного неравенства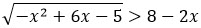 я сначала отмечу, что корнем соответствующего уравнения
я сначала отмечу, что корнем соответствующего уравнения
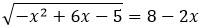
будет единственное число 3 (см. предыдущее решение). Само это число 3, как и число 1, конечно, не является решением данного неравенства. Число же 5, наоборот, является решением данного неравенства.
Число 3 разбивает ОДЗ на два промежутка

На каждом из этих промежутков данное неравенство либо выполняется, либо не выполняется.
Чтобы выяснить это возьмем два числа из этих промежутков: 2 и 4.
При х = 2 данное неравенство не выполняется (проверьте самостоятельно), значит оно не выполняется и на всем промежутке [1; 3].
При х = 4 наше неравенство выполняется, значит оно выполняется и на всем промежутке (3; 5].
Ответ: (3; 5].
Решение II реализовано при помощи так называемого метода интервалов.
Однако ни Решение I, ни Решение II мне не нравятся. Однако это только мое субъективное мнение. И все же мне по душе третье решение данного неравенства.
Решение III.
Это решение - графическое. Для этого надо построить графики двух функций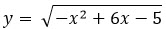 и y = 8 - 2x.
и y = 8 - 2x.
Однако заметим, что
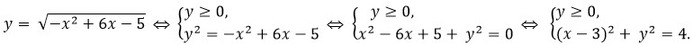
Последняя система задает верхнюю полуокружность с центром в точке (3; 0) и радиусом 2.
После построения в системе координат получим

Не трудно убедиться в том, что точка (3; 2) лежит как на прямой, так и на полуокружности.
Для решения нашей задачи нам нужно найти те значения переменной х, при которых часть полуокружности расположена строго выше части прямой. Это условие выполняется только при х ∈ (3; 5].
Ответ: (3; 5].
Это решение, на мой взгляд, самое лучшее из всех трех решений, которые я привел в этой заметке.
Примечание. Последнее решение не только наглядное, но и позволяет составлять аналогичные задачи учителю и учащимся. Парадокс не задача, не ее текст, а найденное решение реализует технологию развивающего обучения.
В завершение я хотел бы предостеречь моих читателей от типичного заблуждения относительно этих трех решений.
Многие ученики считают, что им нужно освоить, например, только прием из третьего решения, так как оно им нравится. Также есть учителя (и их не мало), которые считают, что им нужно рассказывать своим ученикам только третье решение, так как оно самое изящное, а о двух других решениях не стоит даже вспоминать.
Скажу сразу, что неправы все, как ученики так и учителя. Для того, чтобы стать профессионалом своего дела надо знать все решения данной задачи, даже если некоторые из них не являются рациональными в данном случае. Может случиться так, что прием третьего решение будет трудно реализовать в то время как приемы первого или второго решений останутся единственными из возможных.
В качестве примера рассмотрим неравенство, заимствованное из книги И. И. Мельникова, И. Н. Сергеева "Как решать задачи по математике на вступительных экзаменах" (стр. 89). Скачать эту книгу можно отсюда: https://yadi.sk/d/G1wJWAxFeNqgG.
Решите неравенство
Решение I. Найдем сначала ОДЗ данного неравенства, то есть решим неравенство -х2 + 6х - 5 ≥ 0.
Для этого найдем корни квадратного трехчлена -х2 + 6х - 5. Эти корни мы получим после решения уравнения
-х2 + 6х - 5 = 0,
х2 - 6х + 5 = 0,
D = 36 - 20 = 16 = 42,
x1 = (6 + 4)/2 = 5,
x2 = (6 - 4)/2 = 1,
-(x - 5)(x - 1)≥ 0,
(x - 5)(x - 1)≤ 0.
Решением последнего неравенства будет отрезок [1; 5].
Возводить заданное неравенство в квадрат можно только в случае, когда правая и левая ее части неотрицательны. Поэтому на найденном ОДЗ приходится разбирать два случая.
Рассмотрим первый случай, включая туда и ОДЗ.
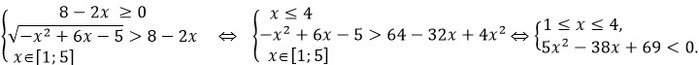
Решим неравенство 5x2 – 38x + 69 < 0.
5x2 – 38x + 69 = 0, D = 1444 – 1380 = 64,
x = (38 ± 8)/10, x1 = 3, x2 = 4,6;
5(x - 3)(x – 4,6) < 0,
Так как х ≤ 4, то x – 4,6 < 0 и х – 3 > 0, x > 3. Поэтому х ∈ (3; 4].
теперь второй случай также включая в него ОДЗ.
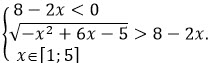
При 8 - 2х < 0 неравенство
(3; 4] U (4; 5] =(3; 5].
Ответ: (3; 5].
Вот такое решение, конечно по стилю, приводится в указанном выше пособии.
Сейчас я покажу другое решение этого же неравенства.
Решение II.
Не повторяясь отмечу, что ОДЗ данного неравенства - отрезок [1; 5].
Вместо данного неравенства
будет единственное число 3 (см. предыдущее решение). Само это число 3, как и число 1, конечно, не является решением данного неравенства. Число же 5, наоборот, является решением данного неравенства.
Число 3 разбивает ОДЗ на два промежутка
На каждом из этих промежутков данное неравенство либо выполняется, либо не выполняется.
Чтобы выяснить это возьмем два числа из этих промежутков: 2 и 4.
При х = 2 данное неравенство не выполняется (проверьте самостоятельно), значит оно не выполняется и на всем промежутке [1; 3].
При х = 4 наше неравенство выполняется, значит оно выполняется и на всем промежутке (3; 5].
Ответ: (3; 5].
Решение II реализовано при помощи так называемого метода интервалов.
Однако ни Решение I, ни Решение II мне не нравятся. Однако это только мое субъективное мнение. И все же мне по душе третье решение данного неравенства.
Решение III.
Это решение - графическое. Для этого надо построить графики двух функций
Однако заметим, что
Последняя система задает верхнюю полуокружность с центром в точке (3; 0) и радиусом 2.
После построения в системе координат получим

Не трудно убедиться в том, что точка (3; 2) лежит как на прямой, так и на полуокружности.
Для решения нашей задачи нам нужно найти те значения переменной х, при которых часть полуокружности расположена строго выше части прямой. Это условие выполняется только при х ∈ (3; 5].
Ответ: (3; 5].
Это решение, на мой взгляд, самое лучшее из всех трех решений, которые я привел в этой заметке.
Примечание. Последнее решение не только наглядное, но и позволяет составлять аналогичные задачи учителю и учащимся. Парадокс не задача, не ее текст, а найденное решение реализует технологию развивающего обучения.
В завершение я хотел бы предостеречь моих читателей от типичного заблуждения относительно этих трех решений.
Многие ученики считают, что им нужно освоить, например, только прием из третьего решения, так как оно им нравится. Также есть учителя (и их не мало), которые считают, что им нужно рассказывать своим ученикам только третье решение, так как оно самое изящное, а о двух других решениях не стоит даже вспоминать.
Скажу сразу, что неправы все, как ученики так и учителя. Для того, чтобы стать профессионалом своего дела надо знать все решения данной задачи, даже если некоторые из них не являются рациональными в данном случае. Может случиться так, что прием третьего решение будет трудно реализовать в то время как приемы первого или второго решений останутся единственными из возможных.
Серия сообщений "Методические статьи":
Часть 1 - О ПУТАНИЦЕ В ТЕРМИНОЛОГИИ: Решение уравнения и Корень уравнения
Часть 2 - МАТЕМАТИЧЕСКАЯ ОШИБКА В ШКОЛЬНОМ УЧЕБНИКЕ
...
Часть 15 - Рисунок-ключ к решению текстовой задачи
Часть 16 - Угол между двумя плоскостями. Задание 16(С2)
Часть 17 - Неравенства с радикалами
Часть 18 - О методическом мастерстве
Часть 19 - Квадратные уравнения
|
Формирование теоретического мышления. Часть I |
Дневник |
Пример формирования эмпирического мышления
 Эмпирическое (опытное) мышление и познание представляет собой деятельность, в основе которой преобладает живое, непосредственное созерцание объекта.
Эмпирическое (опытное) мышление и познание представляет собой деятельность, в основе которой преобладает живое, непосредственное созерцание объекта.Оно прежде всего сохраняет свою связь с восприятием. В ходе эмпирического мышления познаваемый объект отражается со стороны его внешних связей и свойств. В процессе познания познающий ориентируется на внешние условия существования объекта и на то содержание в нем, которое прямо доступно восприятию и наблюдению.
Результатом эмпирического мышления выступает знание непосредственного в действительности. В таком знании отражаются внешние сходные черты познаваемых объектов, но не его внутренняя сущность скрытая от внешнего созерцания.
Рассмотрим пример из обычной практики преподавания математики в средней общеобразовательной школе.
Решить уравнение

Эта задача кочует из одного методического пособия в другое. В прекрасном сборнике задач [1] предлагается такое решение.
Поделим числитель и знаменатель дроби, расположенной в левой части уравнения на х2, конечно, предварительно проверив число 0 на роль корня уравнения. После выполнения этой операции получим

Введем теперь обозначение х + 1/x = y, тогда наше последнее уравнение примет вид
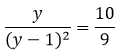
10y2 - 20y +10 = 9y, 10y2 - 29y +10 = 0, D = 292 - 4 ⋅ 10 ⋅ 10 = 841 - 400 = 441 = 212, y1 = 0,8; y2 = 2,5.
Если y1 = 0,8; х + 1/x =2/5; 5x2 - 2x + 5 = 0. Это уравнение не имеет действительных корней.
Если y2 = 2,5; х + 1/x =5/2; 2x2 - 5x + 2 = 0; D = 25 - 4 ⋅ 2 ⋅ 2 = 32, x1 =1/2; x2 = 2.
Ответ: 1/2; 2.
Это типичный пример формирования эмпирического мышления учащихся, т . к. практика преподавания математики в современной школе предполагает после такого решения этого уравнения рассмотренным выше способом решение еще нескольких таких же аналогичных уравнений для того, чтобы учащиеся прочно овладели соответствующими навыками. Это и называют в современной школе закреплением.
Ни в пособии [1], ни в других пособиях, содержащих рассмотренное выше уравнение (или аналогичное) не проводится анализа решения.
Действительно, почему надо делить числитель и знаменатель дроби из левой части данного уравнения на х2. Это что новый метод? А может ничего нового здесь нет? А как рассмотренный прием (деления на х2) согласуется с ранее приобретенными знаниями учащихся? Может быть мы уже применяли этот способ?
Все эти вопросы остаются без ответа. Нет даже попытки авторами методических пособий сформулировать эти вопросы. Типичный признак эмпирического преподавания математики: запомни, повтори, примени много много раз. Так и здесь.
В терминах классической методики преподавания математика здесь мы наблюдаем нарушение принципа научности. Действительно, НАУКА - это сфера человеческой деятельности, функция которой — выработка и теоретическая систематизация объективных знаний о действительности. Поэтому не ясно к какой системе знаний относятся метод решения этого уравнения.
Наука охватывает не только деятельность по получению нового знания, но и результаты этой деятельности — систему научных знаний, которая лежит в основе научной картины мира. Поэтому любые новые знания должны находиться в определенной связи с ранее полученной информацией или относится к новому разделу науки.
Другими словами, наше уравнение и его методы решения должны входить в систему знаний об уравнениях вообще и в систему знаний о некоторых, ранее изученных типах уравнений, так как только в этом случае образуется совокупность элементов, взаимосвязанных друг с другом и таким образом образующих определенную научно организованную целостность.
О том, что автор, предложивший этот метод решения нашего уравнения открыл нечто новое, еще неизвестное другим трудно себе представить. Наверное его "метод" - это нечто вырванное из контекста ранее известного.
Такой рецептурный подход преподавания математики изжил себя уже давно. Действительно, что будет, если так мы будем поступать со всеми уравнениями - предлагать для каждого из них "свой" рецепт решения. Выдержит ли память у учеников? Ведь она не безгранична! Сколько же нужно при этом тупо, механически запомнить и сколько нужно потратить времени на соответствующую тренировку чтобы как-то усвоить эти многочисленные доморощенные "методы".
Думаю, что поставленные мной вопросы говорят о том, что так преподавать математику сегодня нельзя. Нельзя даже описывать решения известных задач. В этом плане стоит поучиться у Л. Эйлера, который значительную часть своих статей посвящал описанию того как он получал решения научных вопросов и тому с какими известными задачами связано его решение.
В этой заметке я только критикую сложившуюся практику преподавания математики и не даю ответа на вопрос о том, как же надо преподавать математику, даже на примере решения на уроке рассмотренного выше уравнения. Это и будет целью моих следующих заметок, но уже закрытого типа.
Литература
1. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учебн. пособие для 10 кл. сред. шк. - М., Просвещение, 1989.
|
| Страницы: | [1] |






