-–убрики
- ћетодические статьи (44)
- –азвивающее обучение (16)
- јрифметика (7)
- јлгебра (4)
- «адачи на клетчатой бумаге (4)
- ѕроценты (2)
- “ригонометри€ (1)
- ћои инструменты (29)
- Kandidat CMS (4)
- »нтернет (4)
- Skype (3)
- Online доски (2)
- Youtube (2)
- Ёлектронна€ почта (2)
- ‘отошоп (2)
- –ешени€ тестов ≈Ќ“ (14)
- ”роки решени€ тестов ≈Ќ“ (5)
- урс HTML5 и CSS3. II. ѕрограммы и настройки (4)
- урс HTML5 и CSS3. I. ¬ведение (4)
- ¬ерстка сайта (4)
- Ѕытовые наблюдени€ (3)
- ‘ункциональные уравнени€ (3)
- ћои »нтернет-проекты (3)
- –ецензии (3)
- “еори€ веро€тностей (2)
- «адани€ типа ¬10 (2)
- ћетод координат в задачах ≈√Ё (2)
- омбинаторика (1)
- PHP (1)
- ”–— HTML5 » CSS3. III. “≈ —“ (0)
- –ешени€ задач (30)
- –ешени€ тестов ≈√Ё (31)
- «адание типа ¬3 (2)
- —тарые записи о »нтернет-проектах (4)
-ћетки
-ѕоиск по дневнику
-ѕодписка по e-mail
-—татистика
ƒругие рубрики в этом дневнике: ‘ункциональные уравнени€(3), “еори€ веро€тностей(2), —тарые записи о »нтернет-проектах(4), –ешени€ тестов ≈Ќ“(14), –ешени€ тестов ≈√Ё(31), –ецензии(3), ћои »нтернет-проекты(3), ћои инструменты(29), ћетодические статьи(44), ћетод координат в задачах ≈√Ё(2), ”–— HTML5 » CSS3. III. “≈ —“(0), урс HTML5 и CSS3. II. ѕрограммы и настройки(4), урс HTML5 и CSS3. I. ¬ведение(4), омбинаторика(1), ¬ерстка сайта(4), Ѕытовые наблюдени€(3), PHP(1)
«адача —5 с параметром |
ƒневник |
Ёта задача относитс€ к классу задач о расположении корней квадратного трехчлена с параметром относительно некоторого числа ј. ¬озможны три случа€: оба корн€ меньше ј; один корень меньше ј, а другой - больше ј; оба корн€ больше ј.
ƒл€ решени€ таких задач имеетс€ три подхода. ѕервый подход опираетс€ на специально разработанную теорию, котора€ содержит алгоритмы решени€ каждой из задач. ¬торой подход сводитс€ к проблеме о определени€ знаков корней квадратного уравнени€. Ёто делаетс€ при помощи подстановки х = t +A, в результате которой трехчлен относительно х переходит в трехчлен относительно t. «наки корней нового уравнени€ очевидным образом определ€ют расположение корней квадратного уравнени€ относительно числа ј. “ретий подход основан только на той теории, котора€ изучаетс€ в общеобразовательной школе.
–ешение I. ѕусть х = t + 1. “огда (t + 1)2 + 2(а - 1)(t + 1) + а2 - 8а + 9 = 0, t2 + 2t + 1 + 2(a - 1)t + 2a - 2 + а2 - 8а + 9 = 0, t2 + 2at + а2 - 6a + 8 = 0.
“ак как корни уравнени€ х1 и х2 должны удовлетвор€ть неравенствам х1 = t1 + 1< 1 и х2 = t2 + 1 < 1, t1 < 0 и t2 < 0. ѕоэтому наша задача может быть переформулирована так: "ѕри каких значени€х параметра а уравнение t2 + 2аt + а2 - 6а + 8 = 0 имеет два отрицательных корн€?"
ƒл€ этого необходимо и достаточно чтобы выполн€лись неравенства: D > 0 (корни существуют), а2 - 6а + 8 > 0 (оба корн€ одного знака), -2a < 0 (сумма корней отрицательна, значит они оба отрицательные).
D = а2 - а2 + 6a - 8 > 0, 6a > 8, a > 4/3.
а2 - 6а + 8 > 0 ⇔ a ∈ (-∞; 2) ∪ (4; +∞).
-2a < 0, a > 0.
«начит, a ∈ (4/3; 2) ∪ (4; +∪).
–ешение II. “еори€ о расположении корней квадратного трехчлена относительно некоторого числа (в нашем случае относительно числа 1) изложена в книге √.¬. ƒорофеева " вадратный трехчлен в задачах". Ёту книгу можно прочитать по адресу http://lib.mexmat.ru/books/85823 или скачать тут: http://yadi.sk/d/HOUu5ZFc9Ctyh или http://www.mediafire.com/?hb256u403irue3t или http://ifolder.ru/21421132 . ј если не удастс€ ее найти по указанным адресам, то наберите в строке поиска в ya.ru текст "скачать ƒорофеев √.¬. вадратный трехчлен в задачах" и вы об€зательно скачаете или прочитаете эту книгу и, использу€ соответствующие формулы, решите нашу задачу..
я считаю, что дл€ решени€ нашей задачи, а значит, и всех аналогичных задач, не нужно знать особых подходов, достаточно владеть теорией решени€ квадратных уравнений излагаемой по программе общеобразовательной школы.
–ешение III.
ј это мое решение, которое не использует замысловатых теорий, основано на самых простых знаний школьного курса математики общеобразовательных классов.
я бы еще предложил вы€снить, при каких значени€х параметра а уравнение х2 + 2(а - 1)х + а2 - 8а + 9 = 0 имеет два корн€ каждое из которых больше 1; один корень больше 1, а другой меньше 1 и оба корн€ принадлежат, например, промежутку (1; 4).
ћетки: ≈√Ё —5 |
«адача о двузначном числе |
ƒневник |
 „ита€ книгу посв€щенную методике преподавани€ математики (√.ѕ. Ѕевз. ћетодика розв'€зуванн€ алгебрањчних задач у 6-8 класах) € встретил простую задачу, котора€ имеет несколько интересных и полезных в методическом отношении (дл€ логического развити€ учащихс€) решений. ¬от условие этой задачи в моем вольном переводе с украинского €зыка.
„ита€ книгу посв€щенную методике преподавани€ математики (√.ѕ. Ѕевз. ћетодика розв'€зуванн€ алгебрањчних задач у 6-8 класах) € встретил простую задачу, котора€ имеет несколько интересных и полезных в методическом отношении (дл€ логического развити€ учащихс€) решений. ¬от условие этой задачи в моем вольном переводе с украинского €зыка.—умма цифр двузначного числа рана 15. ≈сли это число умножить на 7 и от произведени€ отн€ть двузначное число, записанное теми же цифрами что и данное, но в обратном пор€дке, то получим 387. Ќайти двузначное число.
ѕервое, что € сделал - нашел свое, как мне кажетс€, самое простое решений этой задачи, доступное даже учащимс€ младших классов. ¬от эта задача и ее несколько решений.
–ешение 1.
“ак как сумма цифр двузначного числа рана 15, то возможно это число 69, 78, 87 и 96. Ќе так уж много кандидатов на правильный ответ. “еперь проверим каждое из этих число на выполнение услови€ "≈сли это число умножить на 7 и от произведени€ отн€ть двузначное число, записанное теми же цифрами что и данное, но в обратном пор€дке, то получим 387".
69 ⋅ 7 - 96 = 387. «начит, 69 - искомое число.
ќднако задача может иметь и другие решени€. ѕоэтому проверим оставшиес€ числа (78, 87 и 96) на выполнение этого услови€.
78 ⋅ 7 - 87 (оканчиваетс€ на 9) ≠ 387.
87 ⋅ 7 - 78 (оканчиваетс€ на 1) ≠ 387.
96 ⋅ 7 - 69 (оканчиваетс€ на 3) ≠ 387.
«начит, 69 - единственное искомое число.
ќтвет: 69.
–ассмотренный мною метод решени€ этой задачи называетс€ методом перебора. ќн эффективен тогда, когда кандидатов дл€ выбора среди них не так много.
јвтор, указанной выше книги решает эту задачу следующими двум€ способами.
–ешение 2.
ќбозначим цифру дес€тков искомого двузначного числа через х. “огда цифра его единиц будет 15 - х, поэтому искомое число равн€етс€ 10х + 15 - х; 10(15 - х) + х - число, записанное теми же цифрами, но в обратном пор€дке. ѕолучаем уравнение
(10х + 15 - х) ⋅ 7 - (10(15 - х) + х) = 387.
–ешив это уравнение получим х = 6 (цифра дес€тков). ÷ифра единиц: 15 - х = 9.
ќтвет: 69.
–ешение 3.
ќбозначим цифру дес€тков искомого двузначного числа через х, а цифру единиц - через у. “ак как сумма цифр равна 15, то получаем уравнение х + у = 15. роме этого из услови€ задачи следует еще одно уравнение: (10х + у) ⋅ 7 - (10у + х) = 387, 69х - 3у = 387, 23х - у = 129.
ѕолучаем систему уравнений
котора€ имеет единственное решение х = 6, у = 9.
ќтвет: 69.
¬от такие решени€ предлагает нам автор пособи€ по методике преподавани€ алгебры. Ќе знаю почему, но √.ѕ. Ѕевз не указа еще одного решение рассматриваемой задачи.
–ешение 4.
ќбозначим цифру дес€тков искомого двузначного числа через х, а цифру единиц - через у. »з услови€ задачи следует уравнение: (10х + у) ⋅ 7 - (10у + х) = 387, 69х - 3у = 387, 23х - у = 129, 23х = 129 + у.
“ак как у ≥ 1 (у - перва€ цифра двузначного числа, поэтому у ≠ 0) и у ≤ 9, то 130 = 129 + 1 ≤ 129 + у ≤ 129 + 9 = 138.
ѕоэтому 130 ≤ 23х ≤ 138, 5, 652... ≤ 23х ≤ 6. «начит, х = 6.
23 ⋅ 6 = 129 + у, у = 138 - 129, у = 9.
ќтвет: 69.
ћетки: урок |
»нтеграци€ арифметики и алгебры |
ƒневник |

—реди многочисленных школьных математических задач особо выдел€ютс€ сюжетные задачи. »х также называют текстовыми.
¬ыдел€ют два основных метода решени€ сюжетных задач - арифметический и алгебраический.
ƒо 70-х годов прошлого столети€ основным методом решени€ задач в курсе математики был арифметический метод. ќднако позднее за счет алгебраизации курса математики начальной и неполной средней школы из программы было практически вытеснено изучение разнообразных арифметических приемов решени€ текстовых задач. —амым распространенным методом решени€ задач стал алгебраический.
Ќо еще тогда ј.Ќ. олмогоров предостерегал от чрезмерного увлечени€ алгебраическим методом.
ѕрактика показала справедливость его предупреждени€.¬ насто€щее врем€ еще раз возникла необходимость пересмотра содержани€ обучени€ математике (в частности, арифметике). ¬ последние годы по€вилась методическа€ литература, в которой наметилась тенденци€ возвращени€ к арифметическим способам решени€ задач.
ћне не хотелось бы, что все пошло по замкнутому кругу. аждый из методов решени€ текстовых задач имеет свои преимущества и свои недостатки. ѕоэтому в школьном курсе математики следует изучать оба метода.
ѕример. —умма двух чисел равна 38. Ќайти эти числа, если 2/3 первого числа равны 3/5 второго.
–ешение 1.
ѕусть первое число составл€ет 90 (90 делитс€ на 2, на 3 дважды и на 5) частей. “огда его 2/3 будут равны 60 част€м. 60 : 3/5 = 100 - столько частей составл€ет второе число.
—умма двух чисел равна 90 + 100 = 190 частей. “огда первое число равно 38 : 190 * 90 = 18, а второе - 38 - 18 = 20.
ѕроверка. 2/3 от числа 18 равно 12, а 3/5 от числа 20 составл€ют тоже 12. «начит задача решена верно.
–ешение 2.
ѕусть первое число равно х, а второе - у. “огда

–ешив эту систему мы получим х = 18, а у = 20.
онечно, эту задачу можно было бы решить при помощи только одного уравнени€.
ќднако мне не нравитс€, что в в приведенных выше решени€х арифметический и алгебраический методы "разобщены".
–ассмотрим еще одно решение, в котором оба метода мирно сотрудничают (в отличии от их сторонников и противников).
–ешение 3.
ѕусть первое число равно х, а второе - у. “огда
 .
.«начит, первое число составл€ет 9 частей, а второе - 10. “огда на все число будет приходитьс€ 9 + 10 = 18 частей. ѕоэтому первое число равно 38 : 19 * 9 = 18, а второе - 38 : 19 * 10 = 20.
ѕроверку € пропускаю, но она об€зательный элемент решени€.
ѕоследнее решение мне нравитс€ больше всех, так как здесь реализованы все методические преимущества обоих методов.
ћетки: урок |
«адача из рассказа Ђ–епетиторї јнтона ѕавловича „ехова |
ƒневник |
ќтрывок из рассказа Ђ–епетиторї јнтона ѕавловича „ехова

≈сли помните, в рассказе ј. ѕ. „ехова Ђ–епетиторї гимназист ≈гор «иберов не сумел решить арифметическую задачу, а отец репетируемого им ученика, отставной губернский секретарь ”додов, довольно быстро, пощЄлкав на счЄтах, получил правильный ответ. Ќе смогли бы вы также арифметически решить эту задачу? ¬от она.
- У упец купил 138 аршинов черного и синего сукна за 540 рублей. —прашиваетс€, сколько аршин купил он того и другого, если синее стоило 5 рублей за аршин, а черное 3 рубл€? У ѕовторите задачу.
ѕет€ повтор€ет задачу и тотчас же, ни слова не говор€ начинает делить 540 на 138.
- ƒл€ чего же это вы делите? ѕостойте! ¬прочем, так... продолжайте. ќстаток получаетс€? «десь не может быть остатка. ƒавайте-ка € разделю!
«иберов делит, получает 3 с остатком и быстро стирает.
У —транно...-думает он, ероша волосы и красне€. - ак же она решаетс€? √м!... Ёто задача на неопределенные уравнени€, а вовсе не арифметическа€...Ф
”читель гл€дит в ответы и видит 75 и 63.
..............................................................................................................
-Ёто задача, собственно говор€ алгебраическа€,- говорит он. - ≈е с иксом и игрэком решить можно. ¬прочем, можно и так решить. я вот разделил... понимаете? “еперь вот надо вычесть... понимаете? »ли вот что... –ешите мне эту задачу сами к завтраму... ѕодумайте...
ѕет€ ехидно улыбаетс€. ”додов тоже улыбаетс€. ќба они понимают замешательство учител€. ”ченик 7 класса еще пуще конфузитс€, встает и начинает ходить из угла в угол.
- » без алгебры решить можно, - говорит ”додов, прот€гива€ руку к счетам и вздыха€.
- ¬от, извольте видеть...
ќн щелкает на счетах, и у него получаетс€ 75 и 63, что и нужно было.
Ч ¬от-с... по-нашему, по-неученому.
ак же это "по-неученому" решил эту задачу отставной губернский секретарь ”додов? Ќаверное, не при помощи уравнений или их систем, иначе это стало бы "по-ученому".
Ќаверное, сегодн€ мало кто это сможет сделать. ќтставной губернский секретарь ”додов решал эту задачу чисто арифметическим методом. ¬от как решали в те времена такие задачи.
¬от еще раз условие этой задачи.
упец купил 138 аршинов черного и синего сукна за 540 рублей. —прашиваетс€, сколько аршин купил он того и другого, если синее стоило 5 рублей за аршин, а черное 3 рубл€?
—начала узнаем, сколько заплатил бы купец, если бы купил все 138 аршин по 5 рублей: 138*5=690. Ќа сколько это больше, чем он заплатил? 690-540=150.
“еперь один метр сукна по 5 рублей заменим на сукно по 3 рубл€. ѕон€тно, что затраты купца сократ€тс€ на 5 - 3 = 2 рубл€. “еперь уже переплата станет 150 - 2 = 148 рублей.
—колько же раз таких замен нужно сделать, чтобы ликвидировать переплату в 150 рублей?
Ќетрудно посчитать число таких замен: 150 : 2 = 75.
«начит, в самом начале купцу надо было купить 75 метров сукна по 3 рубл€ и 138 - 75 = 63 метра по 5 рублей.
¬от такое простое решение. ¬озникает риторический вопрос: "Ќужно ли учить таким методам решени€ задач современных школьников?". Ќетрудно ответить - ƒа!
„тобы закрепить в сознании читателей этой заметки рассмотренный выше арифметический метод решени€ этой задачи предлагаю продолжить другое (тоже арифметическое) решение этой задачи.
—начала узнаем, сколько заплатил бы купец, если бы купил все 138 аршин по 3 рубл€: 138 * 3 = 414. Ќа сколько это меньше, чем он должен был заплатить? ...
» еще одна задача на прощание.
Ќа дворе бегают куры и порос€та, у всех вместе 20 голов и 52 ноги. —колько всего кур и порос€т?
∆елаю удачи и не получить умственного переутомлени€!
—ери€ сообщений "ћетодические статьи":
„асть 1 - ќ ѕ”“јЌ»÷≈ ¬ “≈–ћ»ЌќЋќ√»»: –ешение уравнени€ и орень уравнени€
„асть 2 - ћј“≈ћј“»„≈— јя ќЎ»Ѕ ј ¬ Ў ќЋ№Ќќћ ”„≈ЅЌ» ≈
...
„асть 12 - ÷ентр окружности, описанной около четырехугольника
„асть 13 - Wolfram Alpha дл€ браузера
„асть 14 - «адача из рассказа Ђ–епетиторї јнтона ѕавловича „ехова
„асть 15 - –исунок-ключ к решению текстовой задачи
„асть 16 - ”гол между двум€ плоскост€ми. «адание 16(—2)
„асть 17 - Ќеравенства с радикалами
„асть 18 - ќ методическом мастерстве
„асть 19 - вадратные уравнени€
|
«адание типа —6 ≈√Ё-2012 |
ƒневник |

Ќатуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по
крайней мере два числа. ƒл€ каждой группы наход€т сумму чисел этой группы. ƒл€ каждой
пары групп наход€т модуль разности полученных сумм и полученные 6 чисел складывают.
а) ћожет ли в результате получитьс€ 0?
б) может ли в результате получитьс€ 1?
в) акое наименьшее возможное значение полученного результата?
–ешение читайте эдесь.
|
«адание типа —6 о целых числах |
ƒневник |

ƒокажите, что а не может быть четвертой степенью натурального числа, если а - 5 делитс€ на 9.
–ешение. ƒопустим противное, т.е. что а = х4 и а - 5 = 9у, это значит, что уравнение
х4 = 9у + 5. (1)
имеет хот€ бы одно решение в натуральных числах.
ак известно, любое натуральное число х можно представить в виде х = 9*p+r, где 0≤ r < 9, где r и p натуральные, тогда х4= (9p + r)4= 9S + r4. ѕодставл€ем это значение х4 в уравнение (1):
»з последнего равенства имеем r4 - 5 = 9*(у - S), это означает, что r4 - 5 делитс€ без остатка на 9.
ќсталось показать, что этого не может быть, а именно переберем все числа дл€ r = 0, 1, 2 .... , 8. ”бедитесь самосто€тельно в том, что в каждом из этих случаев r4 - 5 не делитс€ без остатка на 9.
«начит, число а - 5 не делитс€ на 9 ни при каких натуральных значени€х а.
|
«адание типа —2 ≈√Ё 2012 года |
ƒневник |
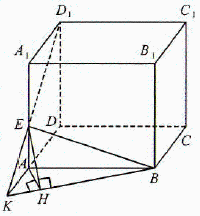
¬ правильной четырЄхугольной призме ABCDA1B1C1D1 стороны основани€ равны 2, а боковые ребра равны 5. Ќа ребре AA1 отмечена точка E так, что AE : EA1 = 3 : 2. Ќайти угол между плоскост€ми јBC и BED1.
–ешение. ѕусть пр€ма€ D1E пересекает пр€мую AD в точке K. “огда плоскости ABC и BED1 будут пересекатьс€ по пр€мой KB.
»з точки E опустим перпендикул€р EH на пр€мую KB, тогда отрезок AH (проекци€ EH) будет перпендикул€рна пр€мой KB (теорема о трех перпендикул€рах).
”гол AHE €вл€етс€ линейным углом двугранного угла, образованного плоскост€ми ABC и BED1.
ѕоскольку AE : EA1 = 3 : 2, получаем:
»з подоби€ треугольников ј1D1E и AKE получаем:
¬ пр€моугольном треугольнике AKB с пр€мым углом A: ј¬ = 2, ј = 3,
»з пр€моугольного треугольника AHE с пр€мым углом A получаем:
ќтвет: arctg(√13/2).
1. ¬ пр€моугольном параллелепипеде ABCDA1B1C1D1 AB1 = 2, AD = AA1 = 1. Ќайдите угол между пр€мой ј¬ и плоскостью ј¬—1.
2. ¬ пр€мой шестиугольной призме ABCDEFA1B1C1D1E1F1 все углы равны 1. Ќјйдите рассто€ние от точки ¬ до плоскости DEA1.
3. ¬ пр€моугольном параллелепипеде ABCDA1B1C1D1 AB = 1, AA1 = 2. Ќайдите угол между пр€мой ј¬1 и плоскостью ј¬—1.
|
«адание типа —6 о коробках |
ƒневник |

»меютс€ 25 коробок, массой 13 кг кажда€ и 19 коробок, массой по 29 кг кажда€. ¬се эти коробки раскладываютс€ по двум контейнерам. ѕусть S Ц модуль разности суммарной массы коробок в контейнерах. Ќайдите наименьшее значение S, если
a) дополнительно требуетс€, чтобы в контейнерах находилось одинаковое количество коробок.
б) без дополнительного услови€ п.а)
–ешение. ѕусть в первом контейнере находитс€ x коробок массой 13 кг и y коробок массой 29 кг. “огда во втором контейнере будет находитс€ соответственно по 25 - x и по 19 - y коробок.
ѕоэтому модуль разности суммарной массы можно записать: S=|13x + 29y - ((25 - x)⋅13 + (19 - y)⋅29)| или S=2⋅|13x + 29y - 438|.
a) ”словие равенства количества коробок выражаетс€ в виде равенства x + y = (25 - x) + (19 - y), 2x + 2y = 44, x + y = 22.
“огда выражение дл€ модул€ разности суммарной массы коробок в контейнерах запишетс€ S=2⋅|13x + 638 - 29x - 438|=16⋅|25 - 2x|.
ѕоскольку S ∈ Z, то минимальное значение выражени€ |25 - 2x| может быть сделано равным только единице, поэтому ответ на п.а) равен 16 .Ётот результат достигаетс€ при x= 12 или x=13.
б) ћинимальное значение выражени€ S=2⋅|13x + 29y - 438| равно 0. „тобы узнать при каких значени€х х и у это значение достигаетс€ нужно решить уравнение 13x + 29y = 438 в целых числах.
13x = 438 - 29y,
“ак как х - целое число, то
9 - 3y = 13k, где k - целое число.
13k + 3y = 9,
¬ силу того, что у тоже целое число, то k = 3t.
»з (2) следует, что у = 3 - 4 ⋅ 3k + k, y = 3 - 13k.
»з (1) получаем, что x = 33 - 2(3 - 13k) + 13 ⋅ 3t = 27 + 29t.
»так, x = 27 + 9t, у = 3 - 13k.
“ак как 0 ≤ х ≤ 9, то 0 ≤ 27 + 29t ≤ 9, -27 ≤ 29t ≤ -2, 0 ≤ x 0.
ѕоследнее неравенство не имеет решений в целых числах. «начит, уравнение 13x + 29y = 438 не имеет решений в целых числах, дл€ х ∈ [0; 25]. ѕоэтому S не может принимать значение 0. ѕоскольку S четное число, наименьшее значение S может быть равно 2. ƒл€ этого найдет решение уравнени€ 13x + 29y - 438 = ±1.
”равнение 13x + 29y = 438 + 1, 13x + 29y = 439 имеет решение х = 7 и у = 12 (решети самосто€тельно по предыдущему образцу). «начит, разность масс контейнеров будет равна 2.
ќтвет: а) 16, б) 2.
1. »меетс€ 33 коробки массой 19 кг кажда€ и 27 коробок массой 49 кг кажда€. ¬се эти коробки раскладывают по двум контейнерам. ѕусть S - модуль разности суммарных масс коробок в контейнерах. Ќайдите наименьшее значение S:
a)если дополнительно требуетс€, что в контейнерах должно находитс€ одинаковое количество коробок;
b)без дополнительного услови€ пунка a.
2.»меетс€ 17 коробок массой 37 кг и 25 коробок массой 61 кг кажда€. ¬се эти коробки раскладывают по двум контейнерам. ѕусть S - модуль разности суммарных масс коробок в контейнерах. Ќайдите наименьшее значение S:
a)если дополнительно требуетс€, что в контейнерах должно находитс€ одинаковое количество коробок;
b)без дополнительного услови€ пункта a.
3.»меетс€ 27 коробок массой 17 кг и 19 коробок массой 61 кг кажда€. ¬се эти коробки раскладывают по двум контейнерам.ѕусть S - модуль разности суммарных масс коробок в контейнерах. Ќайдите наименьшее значение S:
a)если дополнительно требуетс€, что в контейнерах должно находитс€ одинаковое количество коробок;
b)без дополнительного услови€ пункта a.
4.»меетс€ 25 коробок массой 31 кг и 15 коробок массой 51 кг кажда€. ¬се эти коробки раскладывают по двум контейнерам. ѕусть S - модуль разности суммарных масс коробок в контейнерах. Ќайдите наименьшее значение S:
a)если дополнительно требуетс€, что в контейнерах должно находитс€ одинаковое количество коробок;
b)без дополнительного услови€ пункта a.
|
«адание типа —6 из ≈√Ё-2012 |
ƒневник |

Ќайдите все значени€ параметра a, при каждом из которых уравнение 5/(x + 1) = a|x - 4| имеет на промежутке [0;+∞) более двух корней.
–ешение. –ассмотрим графическое решение этой задачи.
¬ообще говор€, известно, что графиком функции y=5/(x+1) €вл€етс€ гипербола. ќднако нас интересует только ее права€ ветвь, которо€ расположена в области [0;+∞). ѕри этом все значени€ функции y=5/(x+1) будут положительными.
√рафик же функции у = a|x-4| стандартен. ѕо условию, данное уравнение должно иметь не менее трех корней. –ассмотрим, при каком расположение графиков функций y=5/(x+1) и у = a|x - 4| на координатной плоскости это возможно.
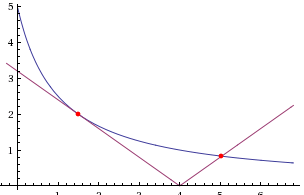
ќпределим точку касани€ гиперболы y=5/(x+1) и графика модул€ у = a|x-4| как это изображено на рисунке выше.
ѕр€ма€ у = -ах + 4 будет касатьс€ гиперболы у = 5/(x+1) только тогда, когда уравнение -а(х - 4) = 5/(x+1) имеет единственное решение. –ассмотрим решение этого уравнени€.
-ах² + 4ах - ах + 4а = 5,
ах² - 3ах - ах - 4а + 5 = 0.
ѕоследнее уравнение имеет единственное решение только тогда, когда его дискриминант равен нулю.
D = 9a² + 4а(4a - 5) = 0,
25a² - 20a = 0,
a = 0 или а = 0,8.
ѕри а = 0 уравнение -а(х - 4) = 5/(x+1) корней не имеет. а = 0,8 удовлетвор€ет нашему требованию (проверьте самосто€тельно!). —лучай а = 0,8 изображен на рисунке выше.
ѕрава€ ветвь модул€ пересекает ветвь гиперболы всегда в одной точке. ѕри a > 0,8 лева€ ветвь графика функции у = a|x-4| будет пересекать ветвь гиперболы в двух точках до тех пор, пока пр€ма€ у = -а(х - 4) будет пересекать ось ординат в точке ниже 5.
ѕр€ма€ у = -а(х - 4) пересекает ось ординат при х = 0 и у = 4а. «начит, 4а < 5< a < 1,25.
ѕоэтому условию данной задачи удовлетвор€ют все значени€ а из промежутка (0,8; 1,25).
ќтвет: (0,8; 1,25).
|
ћножество значений функции в Wolfram|Alpha |
ƒневник |
 ¬ заметке http://www.liveinternet.ru/users/kifar/post224214082/ (ќбласть определени€ функции в Wolfram|Alpha) было подробно описано как находить область определени€ функции одной переменной на примерах решени€ тестовых заданий ≈Ќ“ по математике на базе материалов 2012 года. “еперь настал черед рассмотреть вопрос об определении множества значений функции.
¬ заметке http://www.liveinternet.ru/users/kifar/post224214082/ (ќбласть определени€ функции в Wolfram|Alpha) было подробно описано как находить область определени€ функции одной переменной на примерах решени€ тестовых заданий ≈Ќ“ по математике на базе материалов 2012 года. “еперь настал черед рассмотреть вопрос об определении множества значений функции.
ак и в предыдущей статье мы обратимс€ к материалам тестов ≈Ќ“ (аналог ≈√Ё в азахстане) по математике 2010 - 2012 годов.
ƒл€ начала немного теории. ƒл€ отыскани€ множества значений функции Wolfram|Alpha использует запрос range, который имеет следующий формат:
range f(x)
где range так и переводитс€ как множество значений или область значений; f(x) - конкретна€ функци€, множество значений которой требуетс€ вычислить.
–ассмотрим следующий пример по определению множества значений функции y = ![]() .
.
ак всегда дл€ начала работы перейдем на главную страницу сервиса Wolfram|Alpha по адресу http://www.wolframalpha.com/ и введем запрос в виде range -x^2+8x-3 . Ќа следующем рисунке указано как следует вводить наш запрос и получить на него ответ.

ƒл€ получени€ множества значений нашей функции в окне ввода запросов нажмем на заначек "=". ћы получим интересующий нас ответ

роме этого ответа среди результатов выполнени€ нашего запросы система Wolfram|Alpha изобразить множество значений нашей функции на числовой пр€мой, вычислит область определени€ нашей функции и построит график исследуемой функции в различных масштабах в декартовой системе координат.
|
ќбласть определени€ функции в Wolfram|Alpha |
ƒневник |

ак правило, на экзамене ≈Ќ“ (аналог ≈√Ё в азахстане) в каждом варианте содержитс€ задание на вычисление области определени€ функции. “акие задани€ удобно решать при помощи сервиса Wolfram|Alpha.
ƒл€ вычислени€ области определени€ функции в Wolfram|Alpha есть правило (формат) запроса
где domain буквально переводитс€ как "область определени€ функции", а f(x) - это та функци€, область определени€ которой вам необходимо вычислить. ѕо такому формату запроса система Wolfram|Alpha выводит пользователю: область определени€ функции в терминах теории множеств, ее графическую иллюстрацию и схематическое изображение графика функции. Ётого вполне достаточно, чтобы получить правильный ответ на соответствующее тестовое задание и сверить его с ответами дл€ выбора.
¬от и вс€ небольша€ теори€ по теме "область определени€ функции". ј теперь перейдем к конкретной практике и рассмотрим несколько примеров на вычисление области определени€ функций при помощи системы Wolfram|Alpha. ќтметим лишь, что все эти задани€ вз€ты мной из сборника дл€ подготовки ≈√Ё по математике 2012 года без соответствующих п€ти ответов дл€ выбора правильного среди них.
1. Ќайдите область определени€ функции у = 1/(x² + x).
—начала перейдем на главную страницу сервиса Wolfram|Alpha по адресу http://www.wolframalpha.com/ и введем запрос в виде domain 1/(x^2+x) . Ќа следующем рисунке указано как следует вводить наш запрос и получить на него ответ.

ѕосле указани€ "получить ответ" (нажати€ на кнопку "=") мы получить следующий искомый результат.

ѕон€тно, что это простое задание можно было достаточно быстро решить устно, не прибега€ к помощи Wolfram|Alpha. ≈го мы рассмотрели дл€ того,чтобы объ€снить технику работы по вычислению области определени€ и множества значений функции в системе Wolfram|Alpha.
“еперь рассмотрим решение более сложного задани€.
2. Ќайдите область определени€ функции:
"ѕереведем" это задание на €зык пон€тный системе Wolfram|Alpha: domain 2+sqrt(sin(x/2)). ¬ыполним процедуру получени€ ответа как и в предыдущем примере.
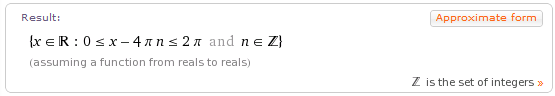
Ётот ответ однозначно соответствует правильному ответу, который содержитс€ в сборнике тестов, откуда был заимствован этот пример.
3. Ќайдите область определени€ функции:

ак видно из рисунка система Wolfram|Alpha дала хот€ и правильный,но не очень корректный ответ: х < -1 или 2х > 1. Ёто, как говоритс€ издержки системы. ¬ообще, на Wolfram|Alpha надейс€, но сам не плошай!
¬от пример, решение которого в системе Wolfram|Alpha никак не соответствует ответам из сборника тестов дл€ подготовки к ≈Ќ“ 2012 года.
4. Ќайдите область определени€ функции у =
«апись данной функции в системе Wolfram|Alpha имеет вид domain sqrt(sin(x)-sqrt(3)cos(x)). ѕолученное решение представлено на следующем рисунке.
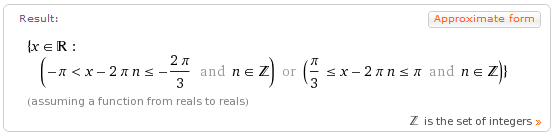
Ёто решение не совпадает ни с одним из ответов дл€ выбора правильного из них в соответствующем тестовом задании. ѕоэтому следует помнить, что система Wolfram|Alpha иногда дает и сбои.
1. Ќайдите область определени€ функции: у =
2. Ќайдите область определени€ функции: у =
3. Ќайдите область определени€ функции:
4. Ќайдите область определени€ функции:
5. Ќайдите область определени€ функции: у = log2(x + 6) + log3(6 - x).
6. Ќайдите область определени€ функции:
ћетки: Wolfram|Alpha ≈√Ё по математике |
Wolfram Alpha дл€ браузера |
ƒневник |

Ќа сайте http://egeent.ucoz.ru € уже опубликовал несколько статей о применении системы Wolfram Alpha дл€ подготовки к ≈Ќ“ и ≈√Ё по математике. ”верен, что такие системы еще не нашили тех, кто их мог бы по достоинству оценить в качестве инструментов преподавани€ учебных дисциплин.
“еперь же € нашел плагины дл€ встройки этой системы в практически любой браузер. “аким образом система Wolfram Alpha всегда у мен€ под рукой (в пр€мом и переносном смысле этого слова). Ёти плагины можно найти по адресу http://www.wolframalpha.com/downloads.html?showall и буквально в один клик мыши установить на своем браузере. оллекци€ плагинов и расширений Wolfram Alpha включает гаджет iGoogle и расширени€ дл€ Firefox, Chrome, Safari, Internet Explorer и Opera.
ѕосле установки соответствующего плагина в правом верхнем углу браузера по€вл€етс€ кнопка соотвествующа€ логотипу системы Wolfram Alpha. ѕосле нажати€ на нее по€вл€етс€ окно дл€ ввода задани€.
“еперь мне нетрудно посмотреть график любой функции типа cos(pi*x) / (-LN2*x), разложение многочлена 2x^5 - 19x^4 + 58x^3 - 67x^2 + 56x - 48 на множители, вычисление значени€ любого громоздкого арифметического выражени€ и т. п.
—ери€ сообщений "ћетодические статьи":
„асть 1 - ќ ѕ”“јЌ»÷≈ ¬ “≈–ћ»ЌќЋќ√»»: –ешение уравнени€ и орень уравнени€
„асть 2 - ћј“≈ћј“»„≈— јя ќЎ»Ѕ ј ¬ Ў ќЋ№Ќќћ ”„≈ЅЌ» ≈
...
„асть 11 - ќкружность описанна€ около трапеции
„асть 12 - ÷ентр окружности, описанной около четырехугольника
„асть 13 - Wolfram Alpha дл€ браузера
„асть 14 - «адача из рассказа Ђ–епетиторї јнтона ѕавловича „ехова
„асть 15 - –исунок-ключ к решению текстовой задачи
...
„асть 17 - Ќеравенства с радикалами
„асть 18 - ќ методическом мастерстве
„асть 19 - вадратные уравнени€
|
»ррациональное неравенство типа —3 |
ƒневник |
 –ешите неравенство
–ешите неравенство 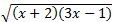 ≤ 1 Ц 2x +
≤ 1 Ц 2x + 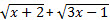 .
.–ешение. Ќайдем ќƒ«.
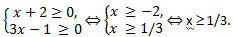
ѕусть
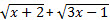 = а, тогда 2 = x + 2 + 2
= а, тогда 2 = x + 2 + 2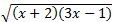 а2 = x + 2 + 2
а2 = x + 2 + 2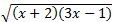 + 3x - 1; >а2 = 4x + 1 + 2
+ 3x - 1; >а2 = 4x + 1 + 2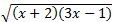 ;
; 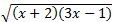 = (а2 - 4x - 1)/2. ѕоэтому данное неравенство примет вид
= (а2 - 4x - 1)/2. ѕоэтому данное неравенство примет вид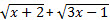 ≤ 3 ⇔
≤ 3 ⇔ 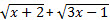 ≤ 3. –ешением последнего неравенства €вл€етс€ промежуток вида [1/3; c], где с - решение уравнени€
≤ 3. –ешением последнего неравенства €вл€етс€ промежуток вида [1/3; c], где с - решение уравнени€ 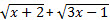 = 3.
= 3.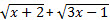 = 3,
= 3,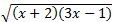 + 3x - 1 = 9,
+ 3x - 1 = 9,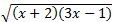 = 8 - 4x,
= 8 - 4x,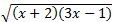 = 4 - 2x,
= 4 - 2x,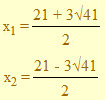
 –ешите неравенство
–ешите неравенство 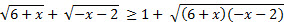 .
.
|
÷елочисленные решени€ системы уравнений |
ƒневник |
–ешение. »з второго уравнени€ данной системы следует, что y - 1 ≥ 0 или у ≥ 1. — учетом того, что у - целое число имеет у ≥ 2.
x²+ 2(y+1)x - 2y + 2y² = x²+ 2(y+1)x + (y + 1)² + y² + y² - 4y < 0 или x² + 2(y+1)x + (y + 1)² + y² - 4y + 4 < 4,
(x + y + 1)² + (y - 2)² < 4.
»з последнего неравенства следует, что (y - 2)² < 4, |y - 2| < 2. “ак как у ≥ 2, то 0 ≤ y - 2 < 2, 2≤ y ≤ 4 . «начит, у = 2 или у = 3.
≈сли у = 2, то данна€ система примет вид
|
–ешение уравнени€ в натуральных числах (¬сесибирска€ олимпиада 2011 года) |
ƒневник |

ќ ¬сесибирской физико-математической олимпиаде школьников € уже писал в одном из своих сообщений. Ёто прекрасный конкурс дл€ школьников 8 - 11 классов. Ќа мой взгл€д, прекрасно организован. —начала учащиес€ участвуют в отборочном online конкурсе, а затем победителей, а их достаточно много, приглашают на очный конкурс. ѕри этом дл€ удобства школьников очные конкурсы проход€т во многих городах –оссии.
Ќиже € привожу свое решение одного из уравнений, предлагавшегос€ на заочном отборочном конкурсе.
Ќайти все решени€ в натуральных числах уравнени€ 2x + 2y = 2z.
–ешение.
≈сли x = y, то 2y + 2y = 2z, 2 ⋅ 2y = 2z, 2y + 1 = 2z, z = y + 1. Ћюба€ тройка (y; y; y + 1), где y - любое натуральное число - решение данного неравенства.
≈сли x > y, то 2x + 2y = 2z, 2y(2x + 1) = 2z. получаем, что четное число 2z делитс€ на нечетное число 2x + 1. „его быть не может.
јналогично доказываетс€, что не имеет место соотношение y > x.
«начит, тройка (y; y; y + 1), где y - любое натуральное число, задает все решени€ данного неравенства.
ќтвет: (y; y; y + 1), где y - любое натуральное число.
|
«адача ¬сесибирской математической олимпиады школьников |
ƒневник |

—начала несколько слов об этой олимпиаде.
¬сесибирска€ физико-математическа€ олимпиада школьников была организована в 1962 году по инициативе академика ћ.ј. Ћаврентьева.
ќсобенностью олимпиады €вл€етс€ также то, что призеры олимпиады приглашаютс€ в Ћетнюю физико-математическую школу, проводимую в јкадемгородке (г.Ќовосибирск), по результатам обучени€ в которой старшеклассники принимаютс€ в физико-математическую школу, ныне —пециализированный учебно-научный центр Ќовосибирского государственного университета.
ѕо –ешению –оссийского совета олимпиад школьников ¬сесибирска€ открыта€ олимпиада школьников включена в ѕеречень олимпиад школьников на 2010/2011 год по математике (2 уровень), физике(2 уровень), химии(3 уровень), биологии (3 уровень) и информатике (2 уровень). Ёто означает, что победители и призеры олимпиад имеют право на получение одной из следующих льгот при поступлении в вузы –‘:
быть приравненными к лицам, набравшим максимальное количество баллов по ≈√Ё по соответствующему предмету;
быть приравненными к лицам, успешно прошедшим дополнительные вступительные испытани€;
быть зачисленными в образовательное учреждение без вступительных испытаний.
ј теперь о задаче.
Ќайти все точки (х; y) координатной плоскости, через которые не проходит ни одна пр€ма€ семейства y = (2px + 1)x - p².
–ешение. ѕусть через точку (х; y) не проходит ни одна пр€ма€ из указанного семейства. Ёто означает, что уравнение y = (2px + 1)x - p² не имеет решений относительно р.
”равнение y = (2px + 1)x - p² запишем как квадратное относительно р: p² - 2хр + y - x = 0.
“ак как последнее уравнение не имеет решений относительно р, то его дискриминант равен нулю, т. е. D = x² - y + x < 0, y > x² + x .
«начит, условию задачи удовлетвор€ют все точки (х; y), дл€ которых y >x² + x . Ёти точки изображены на следующем рисунке.
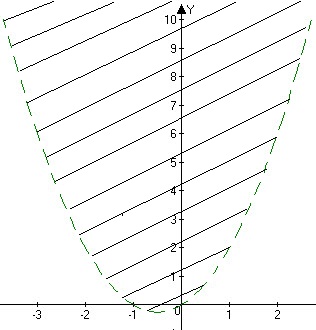
|
‘ункциональное уравнение в тестах ≈√Ё |
ƒневник |
 –аздел — тестов ≈√Ё по математике все больше и больше становитс€ недоступным дл€ учащихс€ обычных общеобразовательных школ. Ќар€ду с задачами повышенной сложности,но все же вход€щими в курс математики обычных школ, там начале по€вл€тьс€ тем€ задач, которые вр€д ли в ближайшие годы будут включены в программы общеобразовательных школ. я имею в виду функциональные уравнени€. Ёта тема относитс€ к так называемым "олимпиадным".
–аздел — тестов ≈√Ё по математике все больше и больше становитс€ недоступным дл€ учащихс€ обычных общеобразовательных школ. Ќар€ду с задачами повышенной сложности,но все же вход€щими в курс математики обычных школ, там начале по€вл€тьс€ тем€ задач, которые вр€д ли в ближайшие годы будут включены в программы общеобразовательных школ. я имею в виду функциональные уравнени€. Ёта тема относитс€ к так называемым "олимпиадным".–адоватьс€ или не радоватьс€ такой моде в тестах ≈√Ё по математике? Ќа мой взгл€д, нет. ƒело в том, что учащиес€ обычных школ даже прочитав услови€ задач типа — начинают чувствовать себ€ не полноценными. “ак дл€ кого же раздел —? онечно, дл€ учащихс€ имеющих повышенную математическую подготовку! «ачем же такие задачи предлагать р€довым учащимс€ и тем самым ставить их в не равноценные услови€ с олимпиадниками?
“аково мое мнение о задани€х типа — в тестах ≈√Ё по математике. ј теперь конкретно к решению примера.
—1. –ешите уравнение g(x) = x3 + 2x² + 4x, если g(2x - 1) = 4x² + 6x - 3.
–ешение. ѕусть 2x - 1 = t, тогда х = (t + 1)/2 и 4x² + 6x - 3 = (t + 1)² + 3(t + 1) - 3 = t² + 5t + 1. «начит, g(x) = x² + 5x + 1.
‘ункцию g(x) можно было бы найти иначе: 4x² + 6x - 3 = (2x - 1)² + 10x - 4 = (2x - 1)² + 5(2x - 1) + 1. ѕусть 2x - 1 = t, тогда g(t) = t² + 5t + 1 или g(x) = x² + 5x + 1.
”равнение g(x) = x3 + 2x² + 4x примет вид x² + 5x + 1 = x3 + 2x² + 4x.
x3 + x² - x - 1 = 0,
x²(x + 1) - (x + 1) = 0,
(x + 1)(x² - 1) = 0.
–ешени€ми последнего уравнени€ будут числа х = ±1.
ќтвет: х = ±1.
C1. –ешите уравнение g(x) = 7x - x³ + 3, если g(x) = 4x² - 6x - 1.
|
–ешение уравнени€ в целых числах (задание ≈√Ё типа —6) |
ƒневник |

¬ задани€х теста ≈√Ё по математике стало модным предлагать учащимс€ решить уравнение в целых числах. Ѕольшинство учащихс€ не имеет даже представлений о том, что есть такие уравнени€. Ѕыло бы разумнее проводить ≈√Ё в два этапа: дл€ всех и дл€ избранных. ѕоследним и надо предлагать такие задани€. ƒл€ основной массы учащихс€ даже не следует показывать такие задани€, так как они подрывают в них уверенность в успешном решении заданий типа ¬.
ќп€ть идет полемика о том, что ≈√Ё надо разделить на два этапа: дл€ всех (выпускной школьный экзамен) и дл€ поступающих в вузы. —нова пришли к разбитому корыту советских времен. » правильно!
ќднако все это мое (школьного учител€) мнение, на которое наши власти не обращали, и, наверное, не будут обращать внимание. ¬едь только им "избранным" следует знать, а главное, решать какими быть школьному экзамену, а мне "сурку" это не дозволено.
ѕосле таких печальных лирических отступлений перейдем теперь к разбору нашего задани€.
—6. –ешите в целых числах уравнение: 1 + 2k + 22k+1 = n2.
–ешение. ≈сли k = 0, то уравнение примет вид 5 =n2 и не имеет решений.
≈сли k = -1, то уравнение примет вид 2 =n2 и тоже не имеет решений.
≈сли k ≤ -2, то 1 < 1 + 2k + 22k+1 < 1 + 14 + 14 < 2 и 1 2 < 2. ¬ этом случае данное уравнение также не имеет решений.
ќстаетс€ рассмотреть случай, когда k - натуральное число. “огда 1 + 2k + 22k+1 ≤ 11 и n - целое неотрицательное число. Ќе тер€€ общности рассуждений можно считать, что n - натуральное число, так как при n < 0 n2 = (-m)2, где m = -n - натуральное число.
2k(1 + 2k + 1) = (n - 1)(n + 1).
ѕон€тно, что n будет нечетным числом. ѕусть n = 2m + 1. “огда (n - 1)(n + 1) = 2m(2m + 2) = 4m(m + 1) и наше уравнение примет вид:
„исла 2k - 2 и 1 + 2k + 1 взаимно просты. ƒействительно, если d их наибольший общий делитель, то число
1 + 2k + 1 - 2 ⋅ 2k - 2 = 1 делитс€ на d. «начит d равно 1.
јналогично доказываетс€, что числа m и m + 1 тоже €вл€ютс€ взаимно простыми.
ѕусть m четное число. “ак как права€ часть уравнени€ (*) делитс€ на m, то и права€ его часть тоже делитс€ на m. “ак как и 1 + 2k + 1 - нечетное число, то 2k - 2 делитс€ на m. ѕри этом права€ часть уравнени€ (*) делитс€ на 2k - 2, значит и его права€ часть тоже делитс€ на 2k - 2. ¬ силу того, что m + 1 - нечетное число, то m делитс€ на 2k - 2. Ќатуральные числа m и 2k - 2 дел€тс€ друг на друга. Ёто возможно только при m = 2k - 2. “огда m + 1 = 1 + 2k + 1 и m = 2k + 1. ѕолучили, что m равно двум различным натуральным числам 2k + 1 и 2k - 1. „его быть не может.
“акже приходит к противоречие, если m + 1 - четное число. “аким образом ни m, ни m + 1 не могут быть четными. Ќо из двух последовательных натуральных чисел одно об€зательно €вл€етс€ четным. «начит, данное уравнение решений в целых числах на имеет.
|
«адача на отношение площадей трапеции (типа —4) |
ƒневник |
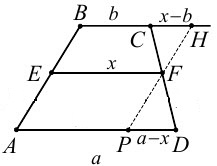
–ешение. Ќеизвестно как относ€тс€ площади трапеций BCFE и AEFD - как 2:3 или как 3:2.
ѕоэтому эту задачу будем решать в общем виде.
ќбозначим искомый отрезок ≈F через х. ѕусть площади трапеций BCFE и AEFD относ€тс€ как m:n.
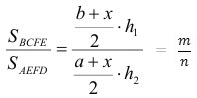 . ќтсюда
. ќтсюда 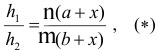
где h1 и h2 - высоты этих трапеций.
„ерез точку F проведем отрезок –Ќ параллельно ј¬ (можно было бы этот отрезок провести через точку — или D). “огда треугольники PFD и CHF подобны (докажите самосто€тельно) и
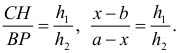
»спользуем соотношение (*):
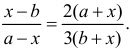
–еша€ полученное уравнение относительно переменной х, получаем m(х² - b²) = n(a² - x²), (m + n)x² = na² + mb²,
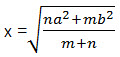 .
.≈сли площади трапеций BCFE и AEFD относ€тс€ как 2:3, то m = 2, n = 3 и искомый ответ будет
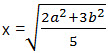 .
.≈сли же площади трапеций BCFE и AEFD относ€тс€ как 3:2, то m = 3, n = 2 и искомый ответ будет
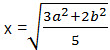
ќтвет:
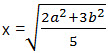 или
или 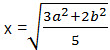 .
.
|
| —траницы: | [2] 1 |






