На это стоит посмотреть!

Владимир Путин - интервью 15 лет назад

ГИПОТЕЗЫ О ПОЛОЙ ЗЕМЛЕ. НА СУД ЗДРАВОМЫСЛИЯ.

Что внутри нашей Планеты?

«Геолог и писатель Сергей Обручев в Земле Санникова высказал мысль о возможном существовании оазиса в Арктике, где мог быть вход в Плутонию – поздемный мир, описанный в романе «Плутония», вышедшим в 30-х годах прошлого века, в котором показан мир за Полярным кругом, отапливавшийся за счет глубинного тепла нашей Планеты. Мир, в котором сохранились мамонты и прочие реликты, где жили люди, не знавшие прелестей (и пакостей) Цивилизации. 

Его идея полой Земли заставила задуматься и английского астронома Эдмунда Галлея. Известный британский астроном и математик сэр Эдмунд Галлей, именем которого названа знаменитая комета, был одним из первых, кто всерьез отнесся к идее полой Земли. Пытаясь объяснить перемещение магнитных полюсов нашей Планеты, он выдвинул любопытную гипотезу. «А что если внутри ее вращаются несколько шаровидных оболочек, вставленных одна в другую, - вопрошал он.- Их вращение с разными скоростями вполне может привести к флуктуациям суммарного геомагнитного поля и, как следствие, к смещению полюсов»... 

 

 

 

 

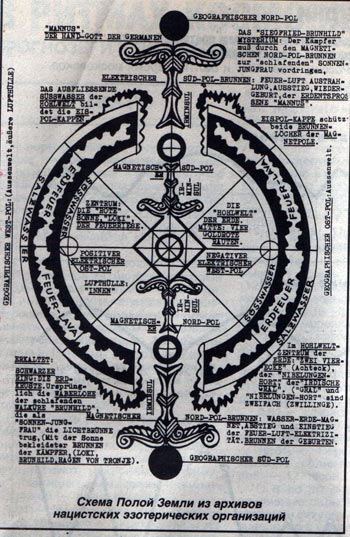
В 1692 году он писал, что Планета представляет собой Оболочку, толщиной около 1000 километров. А внутри – две вложенные друг в друга Сферы, и наконец, ядро Земли, размером с Меркурий. Астроном был твердо убежден, что это «Солнышко» позволило развиться животному и растительному миру на внутренней стороне нашей Планеты. Еще ученый предполагал, что подземная атмосфера, вырываясь в «наш мир», светится. А также он заявил о том, что Земля внутри полая. Между слоями Земли имеется воздух. Все внутренние Сферы имеют собственные магнитные полюса и вращаются в разных направлениях с разной скоростью. Данную теорию Галлей разработал для того, чтобы хоть как-то объяснить аномалии, иногда встречавшиеся в показаниях компасов. Кроме того, он считал, что подземная атмосфера подвержена свечению. В некоторых местах на Севере этот воздух пробивается наружу и вызывает Северные сияния. С тех пор свыше 90% научных теорий подтвердили факты этой книги как правильные. 

Чуть позже идею подхватил один из самых гениальных математиков за всю историю этой науки — слепой швейцарец Леонард Эйлер. Он отказался от концепции внутренних сфер и предположил, что Земля абсолютно пустая, а в центре нее находится Солнце диаметром 600 миль, обеспечивающее светом «продвинутую» Цивилизацию Подземных жителей. Великий математик признавал существование одной полой оболочки - земной коры, отделенной большим пространством от ядра. Она, по его мнению, имеет отверстия на Северном и Южном полюсах. Как считал ученый, такое устройство Земли обеспечивало бы лучшую ее устойчивость, чем наличие нескольких оболочек. Появление модели полой Земли было вызвано необходимостью растолковать некоторые непонятные факты. Так, Кормульс в 1816 году считал, что впадина между Довером и Кале образовалась за счет сдвига коры (толщиной около 500 км) пустотелой Земли. А немецкий профессор Штейнгаузер объяснял Земной магнетизм и его вековые изменения, за счет существования некой внутренней планеты Минервы, медленно двигающейся по круговой орбите внутри земной полости (один оборот за 476 — 480 лет). Эта точка зрения базировалась на высказываниях таких корифеев, как Галлей, Франклин, Лихтенберг. Но раз Земля полая, то почему бы не предположить, что она обитаема не только снаружи, но и изнутри?

Теория полой земли полностью овладела умами теоретиков нацизма, и вплоть до окончания войны они искали вход в подземный мир. Но нацисты верили не только в Полую землю. В апреле 1942 г. они решили проверить еще одну безумную гипотезу, возникшую в 1920 г., – теорию вогнутой земли – о том, что наш мир находится внутри Земли, и жизнь протекает на ее внутренней поверхности. Эту доктрину немецкого авиатора Бендера нацистское руководство восприняло всерьез. Для её проверки лучшие специалисты по радиолокации под руководством доктора Гейнца Фишера высадились на остров Рюген в Балтийском море. Радары были направлены в небо под углом в 45 градусов, и на протяжении многих дней их направление оставалось неизменным. Гитлер надеялся путем отражения получить изображение эскадры английского военно-морского флота, стоящей на якоре в Скапа-Флоу (Северная Шотландия). После неудачной экспедиции на остров Рюген авторитет Бендера упал, а сам он был брошен в концлагерь, где и умер. Основатель Эзотерического общества Грузии Гиви Пирели утверждает, что Гитлер знал о существовании гигантской полости земли, вход в которую находится на Кавказе, и поэтому так стремился захватить Кавказ, наряду, конечно, с бакинской нефтью. О существовании полости он якобы узнал от известного мистика Георгия Гурджиева, эмигрировавшего после революции на запад. Гурджиев учился в семинарии вместе с Иосифом Джугашвили (Сталиным), и в свое время, возможно, рассказал ему о входе в полость-подземелье, которое находится возле местечка Нуниси, возле которого, по словам старожилов, видели Сталина. Верил ли Сталин в подземные миры, мы не знаем, но он приказал расстрелять известного Российского мистика-масона Барченко после его возвращения из экспедиции на Кольский полуостров, организованной КГБ. Что он там искал, до сих пор точно неизвестно, что он нашел – тоже, его материалы до сих пор засекречены. Известно только, что он обнаружил пещеру, вход в которую был после окончания экспедиции взорван им так, чтобы его невозможно было обнаружить. Может быть, это был вход в подземный мир? А что же сейчас? Сейчас сторонники теории Полой земли в качестве аргументов используют фотографии, полученные спутниками НАСА. Согласно общепринятому объяснению, полярное сияние – это свечение разреженных слоев атмосферы под воздействием протонов и электронов, проникающих сверху из космоса, оно как бы опускается к полюсам под воздействием магнитного поля земли. На видеозаписях, взятых на сервере НАСА, четко видно, что южное полярное сияние исходит из отверстия на континенте Антарктида. (Подобные описания северного сияния есть и у полярных исследователей - Нансена и других, писавших, что сполохи сияния поднимаются от горизонта и уходят вверх). Отверстие, подобное гигантской воронке песочных часов, уходящее вглубь Антарктиды, расположено между американской базой Мак-Мердо, Южным полюсом и российской базой «Восток» примерно на 84,4 градуса южной широты и 39 градусов восточной долготы. Интересно, что свечение у полюсов обнаружено и у других планет, существуют снимки свечения полюсов на Меркурии, Венере, Марсе, а также излучение тепла из полюсов на инфракрасном снимке Венеры. Возникает резонный вопрос, почему же эти отверстия до сих пор не найдены? Сторонники гипотезы поясняют, что на самом деле они уже были обнаружены – об этом писал в своих дневниках уже известный нам контр- адмирал Ричард Берд, объявивший, что в 1947 году во время экспедицию в Арктику он попал внутрь Земли и обнаружил там подземных обитателей. Адмирал Берд – руководитель семи научных экспедиций в Арктику в 1926 году и в Антарктиду, начиная с 1929 по 1957 годы. Во время экспедиции в феврале 1947 года он якобы передал по рации, что в районе Северного полюса он видит под собой зеленые леса и загадочных животных, и затем он даже произвел посадку в неизвестном мире и встретился с его обитателями. Об этом он поведал в своих дневниках, опубликованных после его смерти: «11 марта 1947 г . Я только что в Пентагоне рассказал о встрече с королем подземного мира. Сообщение зарегистрировано. О нем доложили президенту. Меня обследуют врачи. А через шесть с половиной часов после моего заявления советник президента приказывает ради блага человечества никогда не рассказывать о том, что я видел в Арктике. Мне напоминают, что я человек военный и должен исполнять приказ… 30 декабря 1956 года. Все эти годы я скрывал великую тайну, хотя это мне и не нравилось. Теперь же я решил, что об этом должен узнать весь мир. В районе Северного полюса есть вход в другой мир!» Но насколько эти дневники подлинны? Ведь в это время Берд как раз находился в Антарктиде, что известно доподлинно, а в марте давал объяснения по поводу своей «странной» войны. Дневники были опубликованы только после его смерти. Возможно, что они были записаны с его слов. Северный полюс был перепутан с Южным, а Арктика – с Антарктидой. По поводу того, что отверстия в полюсах трудно обнаружить, сторонники гипотезы также утверждают, ссылаясь на редкую фотографию Командования воздушно-космической обороны Северной Америки (NOPAD), что траектории орбит спутников, вращающихся над полюсом, проходят не над самым географическим Северным Полюсом – все они проходят сбоку от полюса, огибаяего. Официально сдвиг объясняют тем, что это облегчает слежение, но сторонники гипотезы уверены, что первые полярные спутники вращались точно над полюсом, но при прохождении над ним сходили со своих орбит и разбивались. Нежеланием правительств открывать эту тайну людям объясняют сторонники полой земли и отсутствие фотографий полюсов – только одни белые облака, полностью закрывающие видимость. Странным они считают тот факт, что территория облаков начинается с 83 широты – откуда, по их мнению, начинается полярное отверстие. Все же 23 ноября 1968 года американский космический аппарат ESSA-7 (Environmental Science Service Administration) сделал несколько снимков Северного полюса при полном отсутствии облаков. На этих снимках отчетливо видна огромная черная дыра в районе полюса. Фотографии подлинные – неоднократно проводилась экспертиза. Публикация снимков вновь подогрела интерес к теории о том, что наша планета полая, и там внутри, не исключено, существует другая жизнь. Противников этой невероятной теории намного больше, чем её сторонников. Ученые опровергают ее, пользуясь данными, которыми располагает наука в наши дни: о прохождении сейсмических волн через толщу земли, о средней плотности земли, о прочности пород земной коры, она противоречит современным научным представлениям о зарождении планет путем сгущения газопылевого облака, противоречит теории гравитации… И все же… Как отмечают исследователи, температура по мере приближения к полюсам увеличивается (больше - в Арктике, меньше – в Антарктиде), в северной полярной области океана плавают семена растений, там, где их не должно быть вовсе, причем часто свежие, а не после многих месяцев плавания по океанским просторам; насекомых находят в холодной области недалеко от Северного полюса. Некоторые виды птиц в северном полушарии мигрируют перед зимой на Север – для этого должно быть какое-то основание. Много видов мелких и крупных животных и птиц – тюленей, гусей, уток, кроликов, волков и лисиц присутствуют в крайних северных широтах. Айсберги вокруг Северного полюса состоят из замороженной пресной воды, а не из морской, к тому же, на этих айсбергах встречается красная пыльца неизвестного происхождения. Сплавной лес (включая редкие виды) в изобилии громоздится вдоль побережья Шпицбергена и Гренландии, иногда высота его достигает до 5 метров, и это на 86 градусах северной широты. Мамонт, слон, носорог, бегемот, лев и гиена были найдены во льду около Северного полюса, а на северном побережье Сибири найдено огромное количество гигантской слоновой кости. В желудке замороженных мамонтов находили тропические растения, которые не растут в приполярных областях, причем мясо мамонтов было неиспорченным. Известный тибетский мистик Лобсанг Рампа в своей книге «Сумерки» писал: «В буддизме присутствует понятие Внутреннего мира. Для него даже существует специальное слово – агхарта. Это слово часто используется в священных буддийских текстах. В Тибетской традиции гораздо чаще упоминается Шамбала, в которой живет Король всего мира, скрытый от миллионов, живущих на поверхности. Тибетцы твердо верят, что Король, живущий внутри мира, это не демон – он необычайно добр. Этот духовный правитель вечно существует на двух планах – физическом и духовном. Естественно, на территории Тибета есть тоннели, уводящие глубоко-глубоко. Существует множество легенд о странных людях, приходивших из этих тоннелей и беседовавших с высокопоставленными ламами. … На Земле существует несколько мест, через которые посвященный может пройти к центру Земли и встретиться с представителями внутренней цивилизации. Согласно буддийским книгам, много тысячелетий тому назад начались колебания земной коры, и на многих территориях началось изменение климата. Это изменение вынудило племена перебираться из холодных зон. Во время такого путешествия одно из племен, примерно 25000 лет назад, добралось до места, которое мы сейчас называем Северным полюсом. Они все шли и шли, пока не обнаружили, что солнце всегда висит над их головами, никогда не изменяет своего положения, никогда не поднимается и не опускается. Через некоторое время они поняли, что попали внутрь земли, и открыли, что земля полая». Так какая же она, наша Земля?

 

 

Серия сообщений "НАУКА":
Часть 1 - Киборги на подходе
Часть 2 - В России создан рецепт топлива для гиперзвуковых летательных аппаратов
...
Часть 9 - Самое крупное за десятилетие полное солнечное затмение 20 марта 2015
Часть 10 - 50 лет в открытом космосе
Часть 11 - ГИПОТЕЗЫ О ПОЛОЙ ЗЕМЛЕ. НА СУД ЗДРАВОМЫСЛИЯ.
Часть 12 - Как найти звезды на небе
Часть 13 - Как сделать так, чтобы дети просто обожали вас? Наука в помощь!
Часть 14 - У вас никогда не будет летающего автомобиля и путёвки на Марс, но это ничего
Часть 15 - Гениальнейший монолог. Теория откуда появились люди на Земле

Врата Шамбалы?

То, что искал Гитлер,

спустя десятилетия, обнаружили

местные исследователи...

 

 В разгаре Сталинградская битва и одновременно идут ожесточенные бои за Кавказ. Взявший Ростов горнострелковый корпус генерала Конрада получает неожиданный приказ - бросить две дивизии влево и взять Эльбрус, со стратегической точки зрения интереса не представлявший. Гитлеровские войска держали высочайшую вершину Европы под контролем около пяти месяцев.

Август 1942 года, на стол Гитлера ложится очередная победная реляция об успехах немецких войск на Кавказе. Того, что произойдет с Фюрером после прочтения этого донесения никто не ожидал. Он пришел в ярость, такую ярость, как будто всем его стратегическим планам разом пришел конец. Это была необычная вспышка гнева, припадок длился несколько дней, он кричал и требовать отдать виновных под военный трибунал. Кто были эти виновные?

Что вообще понадобилось Третьему Рейху, в разгар Сталинградской битвы и ожесточенных боев за Кавказ, в пустынном и совершенно стратегически неинтересном районе Эльбруса?

Там работали специалисты Аненербе, искавшие на склонах Священной горы Ариев тайные знания. Тайники на Эльбрусе Гитлер не нашел. Скорее всего, не успел - Эльбрус освободили советские войска... То, что искал Гитлер, спустя десятилетия, обнаружили местные исследователи...

Что за странные древние строения обнаружили исследователи в современное время?

Возвращение и начало

Для настроения





Мы с супругой собираем серию этих открыток
СПАСИБО

Спасибо

Праздники все отдыхаю и работаю за городом. Числа 11, надеюсь ещё застать это удивительное убранство.

Кругооборот к0та числа в Природе :)

 

Серия сообщений "Геометрия мира":

Что в мире есть

Часть 1 - О пользе хотьбы по газонам...
Часть 2 - Слово не воробей... а пуля!
...
Часть 19 - Неразменный рубль. Национальное достояние.
Часть 20 - О кругах на полях
Часть 21 - Кругооборот к0та числа в Природе :)
Часть 22 - Этажи
Часть 23 - Пропульсивный шародвиг
Часть 24 - Авоська :)
 

 

БОЛЕЕ ПОЛНОЕ

[url]http//www.youtube.com/embed/u0eOuxJX36g[/url]

А полное фрактальное обоснование единства Мира смотри в монографии

Г.С. Мельников

Фрактальное единство пространства и времени

ДЛЯ ДРУЗЕЙ - ПРЯМОЙ ВХОД:

С НАСТУПАЮЩИМ 2014 ГОДОМ!!!

 https://cloud.mail.ru/public/56e6f915d48c/GmBH_LAP_Publition_978-3-659-59837-1.pdf

 

Женщины, уставшие рожать солдат...

 

Группа уральских и украинских музыкантов создала антивоенный клип "Женщины устали рожать солдат". За неделю в YouTube ролик посмотрели почти 130 тысяч человек.

Михаил Вексель, один из создателей клипа, утверждает, что на Урале живут идейные подвижники. И вот,его друг и коллега в Челябинске Роман Грибанов однажды позвонил с идеей снять антивоенный клип. В итоге в ролике снялись уральские группы "Братья Енотовы" и "Ариэль", музыкант Гарри Ананасов, украинская "Ревенко-бэнд", а партию гитары исполняет итальянский гитарист Руди Ротта. Михаил Вексель говорит, что потребовалось всего несколько раз слетать в Челябинск, один раз в Италию, в Верону, и видео было готово.

 

Режиссер антивоенного клипа Михаил Вексель – об уважении чувств матерей... 

Читать - здесь

 

В Антарктиде обнаружен вход в подземный мир

1.

ЭТИ И ПРЕДЫДУЩИЕ ДАННЫЕ МЫ РАССМОТРИМ С ЦИТАТАМИ ИЗ МОНОГРАФИИ КОТОРУЮ ВЫПУСТИЛ Международный издательский дом GmBH LAP Publition Г.С. Мельников Фрактальное единство пространства и времени Правосторонний Мир и левосторонний Анти-Мир. GmBH_LAP_Publition_978-3-659-59837-1_ТИТУЛЬНЫЙ_ЛИСТ (700x491, 173Kb)

1.
Внутренняя Земля и её Солнце.

 

 

 

http://www.ezocat.ru/index.php/nauka-ks/1641-zemlya-polaya
 

---

Земля пустая внутри!

 

 

Земля имеет форму шара, пустого внутри, наподобие теннисного мяча.



Толщина Земной коры - 1500км, внутри земной коры находится мантия - именно она извергается из вулканов. Гравитация действует не от центра земли, а от коры, то есть изнутри земная кора притягивает в обратную сторону таким образом, что по внутренней стороне Земли можно ходить так же, как и по внешней.

 

В центре Земли находится ядро или Внутреннее Солнце диаметром 800км, имеющее достаточно энергии, чтобы обогревать внутреннюю часть, лишенную обогрева настоящим Солнцем, однако не такое мощное, чтобы спалить все содержимое.

  

Входы во внутреннюю часть Земли расположены на полюсах - диаметр отверстия несколько сотен километров. Внутренняя Земля обитаема - вполне вероятно, что там живут люди или некто похожий на людей, там намного более комфортный климат, чем на поверхности - постоянная температура и нет сезонности.

Вполне вероятно, что летающие тарелки прилетают вовсе не с других планет или галактик (что часто ставится под сомнение из-за того, что уж очень долго лететь даже со скоростью света), а из центра Земли.

 

Cкорее всего об этом известно правительствам государств и крутым ученым, но скрывается от общественности. Типа как индейцы в америке бы скрывали то, что на том конце океана есть испанские конкистадоры, которые их завоюют если захотят, так как намного сильнее. Зачем такое знать. Читать далее

---

 

Полая Земля.Гипотезы

Читать далее...

Игры, в которые играет Пенроуз

Работа в форме забавы под названием: «А потом прихожу я и говорю вот что…»

Года два тому назад, когда газета «Нью-Йорк Таймс» брала у знаменитого британского ученого Роджера Пенроуза интервью в его рабочем кабинете в Оксфорде, журналистка не могла не обратить внимание на игрушки, тут и там рассованные по комнате. «Зачем это вам здесь?» — последовал вопрос. В ответ на него Пенроуз рассмеялся и обронил: «Наука и забава — вещи неразделимые»…

Довольно сложно пройти мимо того факта, что смысл этого диалога практически точно был воспроизведен тогда же, в 2000 году, и опять же в оксфордских декорациях, но только совсем другими людьми — профессором Дэвидом Дойчем и бравшим у него интервью Леонидом Левковичем-Маслюком.

Дойч сообщил, что работает почти исключительно дома. И тут же уточнил,что «работаю» — это не очень удачное слово для его занятий. Он скорее просто «делает то, что хочется». Решает задачи, смотрит телевизор, программирует, снимает анимационные фильмы, играет в компьютерные игры. Все эти занятия для него, собственно говоря, являются одним и тем же…

Читать далее...

Главная тайна Со-знания

 

очень интересно!

Доступно о гипотизе Пуанкаре

Еще в XIX веке было известно, что если любую замкнутую петлю, лежащую на двумерной поверхности, можно стянуть в одну точку, то такую поверхность легко превратить в сферу. Так, поверхность воздушного шарика удастся трансформировать в сферу, а поверхность бублика – нет (легко вообразить себе петлю, которая в случае с бубликом не стянется в одну точку). Гипотеза, высказанная французским математиком Анри Пуанкаре в 1904 году, гласит, что аналогичное утверждение верно и для трехмерных многообразий.

Доказать гипотезу Пуанкаре удалось только в 2003 году. Доказательство принадлежит нашему соотечественнику Григорию Перельману. Эта лекция проливает свет на объекты, необходимые для формулировки гипотезы, историю поиска доказательства и его основные идеи.

далее с рисунками и пояснениями

НАТАША! Я восхищён Вашими ссылками

Наташа!
Добавлю из последней Вашей ссылки
"Для Роберто Бартини непосредственным толчком к возникновению идеи таблицы, о которой идет рассказ, стало наблюдение того, что множество приборов, устанавливаемых на приборной панели самолета, фиксируют изменение измеряемых величин изменением пространственного положения стрелок и шкал во времени."
На Вашей ссылке
http://www.liveinternet.ru/journal_proc.php?action.../olifirenko47/28965/29162.html
звук в моём ноутбуке в середине просмотра окончательно коротнул (в раздолбанном разъёме) сейчас буду досматривать фильм о Бартини в планшете.
Наташа! Спасибо!
P.S. По Р.О. ди Бартини в последнее время лавинообразно наростают материалы, надо следить постоянно

российское нло




Изобретение не ново.Этим уже занимались.
НЛО Страны Советов
Читать далее...

Песня Дины Гариповой What If для Евровидения. (13,8 МБ)

Только что посмотрел премьеру песни в программе "Воскресное Время" и сразу заливаю сюда.

Будем слушать, привыкать, надеяться и ждать мая месяца...

А перевод песни What If на русский язык смотрим здесь >>>

* * *

 

СТАТЬЯ В СБОРНИКЕ "ВРЕМЯ-2012"

УДК 115
© 2012 г., Г.С. Мельников,

ФГУП «НПК ГОИ ИМ. С.И. Вавилова».

МЕРНОСТИ ПРОСТРАНСТВА-ВРЕМЕНИ.

При поиске мерности пространства-времени необходимо учитывать объективность существования сложной симметрии: зеркально-линзовой 1], объективность существования правосторонних донорных и левосторонних акцепторных структур (мира и антимира), как в геометрии пространства-времени, так и в геометрии социо-структур. Иными словами надо разложить по полочкам побудительные и физические основания этих двух миров:
- Левостороннего и - Правостороннего миров.
фонт=цоуриер]В свете этого понимания автор, как и авторы статьи [2], исходил из построения моделей, основанных на Гамильтоновых гиперкомплексных алгебрах
“Если идти по этому пути, то единственно возможной алгеброй, которая получается из алгебры кватернионов, является семимерная векторная алгебра со скалярным, евклидового характера и векторным произведением двух векторов.
То есть сразу дается ответ на два вопроса: какой размерности должно быть пространство? А это именно семь, не четыре, не пять, не шесть.”[2].
Но, вот с последним утверждением: «А это именно семь…», при более глубоком рассмотрении, вероятно, надо будет распрощаться.
Для понимания, - «почему?», обратимся ещё к двум цитатам. Первое цитирование обращено к соавтору ряда сборников «Время» под ред. В.С. Чуракова, к.т.н. Л.С. Шихобалову
“Направленность времени задает в пространстве-времени определенное направление нормали к нашему Миру (являющемуся в пространстве-времени гиперповерхностью) и тем самым ориентирует наш Мир. В результате правые и левые системы в нем оказываются объективно различными.”[ 3].
Второе цитирование обращено к мыслям гения прошлого, недавнего века - Роберто Орос ди Бартини [4]:
«... в другом сообщении будет показано, что (3+3)-мерность пространства-времени является экспериментально проверяемым фактом и что шестимерная модель свободна от логических трудностей, созданных (3+1)-мерной концепцией».... (Бартини, 1962 год).
Характерно, что введение Р.О. Бартини понятия трёхмерного времени - не только гениальная догадка, но и плод логических выводов. К тому же знаменитые и до настоящего времени не до конца понятые две статьи Р.О. Бартини о цоотношениях между физическими величинами [4] позволили ему исходить в своих рассуждениях из понятий элементарной протяжённости и элементарной длительности. За квант пространства он принимал классический радиус электрона. При этом квант времени в его рассуждениях представлял собой время, за которое свет проходил квант пространства.
Существование дополнительных размерностей времени
Бартини объяснял тем, что время должно характеризоваться не только одной координатой - «положением», но и еще двумя- «скоростью течения» и «ускорением».
Представление, что время имеет «скорость течения» и
«ускорение», можно интерпретировать как существование разных времен, нелинейно связанных друг с другом. Таково, например, время в одной и той же системе, претерпевающей критические изменения. Тогда при переходе от одного времени к другому (от одной системы к другой) время будет менять свою скорость, ускоряться/замедляться и т.д. [5]
Более того, элементарную частицу («элементарный заряд») Бартини
представлял как осциллятор, попеременно являющийся стоком и источником, притом такой, на границе («радиусе формации») которого происходило преобразование пространственных (вещественных) координат в мнимые и обратно. А именно, скорость вращения (обобщённый угол поворота) «формации» на этом радиусе достигала предельного значения, равного скорости света, и при переходе через неё пространственная координата приобретала мнимые («временные») значения, а мнимая временная координата становилась вещественной - то есть превращалась в пространственную. (Здесь Бартини интерпретировал известные формулы преобразования координат и времени Лоренца-Пуанкаре при в > с) /фонт][5].

[ B]Собственные представления автора[/ B]

В своих исследованиях я руководствовался не расплывчатыми обобщенными представлениями, а точной классификацией 192 типов арифметических последовательностей, выводом принципов классификации полюсных многогранников, классификацией и построением программ анализа и синтеза детерминированных двумерных фракталов из кольцевых структур, точного решения задачи математических бильярдов на плоскости. А уже на основании этого базиса решил задачу геометризации пространства-времени, после чего поставил перед собой задачу математических бильярдов в сфере. От классической задачи математических бильярдов в круге задача математических бильярдов в сфере существенно отличается.
Если задача математических бильярдов в круге требует параметрического описания (во времени) движения 2-х точек прямолинейно с отражениями от ограничивающей поверхности круга (механистическая задача), то задача математических бильярдов в сфере требует также параметрического описания движения 2-х точек, но путем решения геометрической задачи построения вписанных многогранников в сферу. При этом осуществлялось построение вписанных полюсных многогранников в сферу в полугеодезической системе координат. Этот выбор обусловлен тем, что при устремлении числа разбиения н по параллелям и числа разбиения к по меридианам к бесконечности, мы с большой точностью приходим к построению главных объектов пространства-времени – полюсным планетам, солнцам, звёздам… В результате всех построений я пришёл к выводу о существовании 16 подпространств шестимерных пространств-времени. (В силу того, что 8 из них конгруэнтны восьми другим, то, в итоге, можно говорить о 8-ми шестимерных пространствах, образующих наш Мир и Антимир.)

В своих работах Р.О. Бартини показал, что размерность пространства метавселенной в математическом описании равна 7, т.е. представляет собой семимерную сферу С7. Принимая одну координату мнимой, он считает остальные 6 измерений реальными. Далее он выделяет 2 подпространства: пространственно-подобной протяженности Л и времени-подобной протяженности Т, каждое из которых получается 3-х мерным. Этими же математическими описаниями пользовался и автор статьи и авторы работы 2], однако, выводы, к которым приходят все авторы, разные.
Действительно, построения многогранников пространства осуществлялось с привлечением кватернионных параметрических уравнений (табл. 1).2012-03-18_ЕВКЛ_НоЕвкл.гиф

Математическое моделирование вписанных многогранников в программах MathCad Professional 3D и Mathematica
Возникает вопрос: единственное ли это представление?
Т.к. в общем случае построения 3Д геометрических фигур (выполнение пространства, по терминологии Е С. Федорова) должны быть не только в кватернионных функциях, но и в октавных, было показано, что построение октав должно предусматривать 16 типов представлений троек векторов для мнимых осей И,Ж и К (рис. 1).2012-03-18_и_ж_к.гиф
&лт;имг срц="//img0.liveinternet.ru/images/attach/c/5/84/920/84920046_20120318_i_j_k.gif" видтх="232" хеигхт="227" алт="2012-03-18_и_ж_к (232х227, 2Кб)" />


При построении этих троек векторов (табл 2.) для центробежных и центростремительных преобразований 3Д фигур на элементарном кубическом объёме получено 16 правил их сочетания (типа правил «левой» и «правой» руки).
Табл 2.
&лт;имг срц="хттп://img0.liveinternet.ru/images/attach/c/5/84/920/84920386_20120318_cenrob_octanti.gif" видтх="416" хеигхт="397" алт="2012-03-18_ценроб_оцтанти (416х397, 11Кб)" />
2012-03-18_центрострем_оцт.гиф

Само же обращение к центростремительным и центробежным движениям обусловлено принципами дискретного преобразования площадей (и объёмов) геометрических фигур с рациональными и иррациональными сторонами (и рёбрами) из фигур с метрикой от Р0 до 0 (центростремительное преобразование), так и от 0 до бесконечности (центробежное преобразование), см рис. 2 и рис. 3.
&лт;имг срц="хттп://img0.liveinternet.ru/images/attach/c/6/91/693/91693340_074.jpg" видтх="600" хеигхт="400" алт="074 (600х400, 29Кб)" />
Рис. 2. Преобразование квадрата путём вписывания в окружности О0, О-1 (центростремительное) и О+1 (центробежное направление)
&лт;имг срц="хттп://img1.liveinternet.ru/images/attach/c/6/91/693/91693453_072.jpg" видтх="600" хеигхт="400" алт="072 (600х400, 25Кб)" />
Рис. 3. Преобразование треугольника путём вписывания в окружности Р, Рком инв (центростремительное) и Рком (центрбежное направление)

Эти построения центробежных и центростремительных троек векторов послужили основанием для введения новых мерностей, а именно: не только тройки пространственных действительных координат, но и динамически меняющегося времени. Время-это всюду плотные концентрические сферы, радиусы которых определяются формулой 1 (по каждой пространственной координате)
Рх,ы,з= Р0(2син(π/к))^ д (1)
Представления вписанных многогранников при бесконечном числе граней в д сферах времени дало мне возможность геометрически представить трактовку модели пространства-времени, введенную гипотезой А. Пуанкаре, в виде динамически меняющейся трёхмерной сферы - бифинслероида (таблица 3). Табл. 3
&лт;имг срц="хттп://img1.liveinternet.ru/images/attach/c/2//72/106/72106122_3D_SF_1.jpg" видтх="158" хеигхт="145" алт=" (158х145, 16Кб)" />
&лт;имг срц="хттп://img1.liveinternet.ru/images/attach/c/6/93/115/93115955_3D_SF_3.jpg" видтх="159" хеигхт="149" алт="3Д_СФ_3 (159х149, 16Кб)" />
&лт;имг срц="хттп://img1.liveinternet.ru/images/attach/c/2//72/106/72106151_3D_SF_2.jpg" видтх="166" хеигхт="149" алт=" (166х149, 17Кб)" />
Эта модель суть - трёхмерная сфера в виде 4-х мерной мгновенной фотографии. Это состояние модели пространства-времени "здесь и сейчас". При «раздувании» трёхмерной сферы во времени (простой пример - рост яблока), введенный амплитудно-угловой множитель Р0/(2син(π/к))^д в октавионных уравнениях вызывает изменения кинематической модели трёхмерной сферы. При этом в модели описываются изменения кривизны пространства-времени. В результате чего трехмерная сфера поочерёдно проходит Евклидовы и не Евклидовы состояния, что соответствует основным представлениям А. Пуанкаре о Евклидовом и не Евклидовом мирах, которые описываются одними и теми же принципами и существуют параллельно.
А. Пуанкаре исходит из предположения, что наша реальная трёхмерная Вселенная обладает свойствами замкнутости (нет "стенок"-"краёв") и односвязности (любое лассо затягивается в точку). На основании этого он предположил, что она обязательно должна быть трёхмерной сферой или деформированной трёхмерной сферой (подобно тому как, например, наша Земля - не идеальный шар, а слегка сплюснута с полюсов).
При моделировании за основу взята интерпретация Пуанкаре, в соответствии с которой плоскость Лобачевского реализуется внутренним пространством круга, а прямые в этом пространстве представляются дугами окружностей, пересекающих основной круг ортогонально. В нашей же модели при решении задачи математических бильярдов эти дуги распространяются в круге зеркально-синфазно с прямолинейными векторами Евклидового мира (Табл. 4)
Табл. 4
&лт;имг срц="хттп://img1.liveinternet.ru/images/attach/c/5/85/360/85360335_026.jpg" видтх="600" хеигхт="400" алт="026 (600х400, 73Кб)" />&лт;имг срц="хттп://img0.liveinternet.ru/images/attach/c/6/91/694/91694480_027.jpg" видтх="600" хеигхт="400" алт="027 (600х400, 39Кб)" />
В интерпретации Пуанкаре метрика пространства вводится с помощью двойных отношений, причем, величины углов на модели такие же, как и на плоскости Лобачевского (модель конформная).
Детальное изучение строения бифинслероида и его динамики (Рис. 4 и табл. 3) позволяет сделать вывод о том, что представленная модель есть дословное описание структуры динамического состояния трёхмерной сферы, которая совпадает с пониманием А. Пуанкаре и Р.О. Бартини о структуре пространства-времени.

&лт;имг срц="хттп://img1.liveinternet.ru/images/attach/c/2//72/132/72132254_Bifinsl_bitetr.png" видтх="335" хеигхт="385" алт=" (335х385, 92Кб)" />

Рис. 4. Бифинслероид
Наглядное представление двойственности с интерпретацией утверждения о том, что мнимая единица — это «квадратный корень из −1», не точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «и», а другой как «-и». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «и» на «-и» и «-и» и на «и». См. также и – угол поворота π/2

На основании сказанного модель бифинслероида есть фигура вращения двух листов Мёбиуса.
Образующие фигуры вращения можно представить в виде резинок, стягивающих банковские пачки банкнот, с шириной, равной краю. В процессе вращения вокруг оси образующие формируют внешние (выпуклые) и внутренние (с отрицательной кривизной ) поверхности бифинслероидов. При этом внешние поверхности бифинслероидов, образующих трёхмерную сферу, будут иметь поверхности, формируемые шириной ленты, а внутренние поверхности, начиная с поворотов на полюсных рукавах на 90 град., формируются в виде поверхностей отрицательной кривизны краями ленты на обоих финслероидах. При этом внешние поверхности верхнего и нижнего финслероидов формируются каждая своим листом Мёбиуса (его шириной), а внутренние поверхности для нижнего финслероида строятся краем верхнего листа Мёбиуса, а для верхнего - краем нижнего листа Мёбиуса.
Усиливая интерпретацию двойственности Мир-Антимир предлагаю рассмотреть физическую модель – планета Земля. Вращение Земли с Северного полюса мы наблюдаем как вращение против часовой стрелки, это же вращение при наблюдении с оси Южного полюса мы интерпретируем как вращение по часовой стрелке. Таким образом, каждый из финслероидов трёхмерной сферы одновременно является действительным и мнимым геометрическим образом.
Всё, что формируется во внутренних поверхностях либо удерживается в виде частиц Антимира в гравитационных (магнитных "бутылках"), либо периодически, как «выдохи» через оси, проходящие через Северный и Южный полюсы (ось не принадлежит нашему Миру), по законам левитации - (материя с отрицательной плотностью), удаляется в виде джетов на периферию Мира. В результате материя с отрицательной плотностью формирует тёмную материю и тёмную энергию.
К пониманию двойственности представлений подходил и Р.О. Бартини. Наиболее полно понятия двойственности изложены в монографии "Тензорный метод двойственных сетей А.Е. Петрова
"Достаточность возникает из инвариантов двойственности. Мощность (поток энергии) остается постоянной (при заданных источниках энергии) при изменении структуры в двойственных сетях. При этом одна сеть располагается в наблюдаемом пространстве, а другая – в двойственном, дополняющем наблюдаемое пространство до целого, более общего пространства. Расщепление единого пространства на два взаимно дополнительных, двойственных составляющих пространства, восстанавливает размерность потока энергии до целочисленных степеней. Поток энергии расщепляется между двумя такими пространствами, в которых при изменении структуры остается постоянной совокупность независимых замкнутых путей и разомкнутых путей. Одна часть потока располагается в соответствующих путях сети одного пространства, а другая часть – в дополняющих путях двойственного пространства. В каждой из частей поток имеет размерность с дробными степенями, а их единство, композиция дает размерность с целыми степенями."
Но надо понимать, что виртуальный мир это не "кажущийся" мир, а реальный параллельный левосторонний мир.
Что касается вопроса не математического моделирования геометрических тел пространства-времени, а физической реализации исследований 7] (помимо уже известных 2-х подпространств с положительным и с отрицательным коэффициентом преломления), даю ещё одну ссылку о возможности физического изучения доселе неизвестных оставшихся 6 подпространств, принадлежащую В.Г. Веселаго (из его интервью 2012 года)
хттп://ufn.ru/ru/ufn90/veselago.html
«Надо заметить, что важность всех этих результатов состоит даже не в том, что можно получить отрицательный коэффициент преломления, а в том, что теперь можно получать композитные материалы с любыми, не обязательно с отрицательными величинами обеих проницаемостей».

Б]ВЫВОДЫ/Б]:

1. Зеркально-синфазное отражение в виртуальном не Евклидовом пространстве траектории Евклидова мира, есть интерпретация А. Пуанкаре не Евклидовой геометрии Лобачевского.
2. Виртуальный мир это не "кажущийся" мир, а реальный параллельный левосторонний мир. Тому полное доказательство в Коллайдерах по обязательному обнаружению пар частиц. (Частиц и Античастиц).
3. Реальное шестимерие Д (3+3) - это дословное описание структуры динамического состояния трёхмерной сферы - состояния пространства-времени в трактовках А. Пуанкаре и Р. О. Бартини, подтверждается приведенным выше динамическим моделированием бифинслероидов.

Б]Библиографичекий список/Б]

1. Мельников Г.С. Время и формирование структур макро- и микромира, Сб. Проблема времени в культуре, философии и науке: сб. науч. тр. / под ред. В.С. Чуракова. (Библиотека времени. Вып. 3). – Шахты: Изд-во ЮРГУЭС, 2006. – 155 с.; Время в динамической модели пространства-времени. Сборник научных трудов под редакцией В.С. Чуракова, Шахты: Изд-во ЮРГУЭС, 2011 г
2. А.В. Коротков и В.С. Чураков. Многомерные концепции пространства и времени (пространства-времени). ,
Сб. Проблема времени в культуре, философии и науке: сб. науч. тр. / под ред. В.С. Чуракова. (Библиотека времени. Вып. 3). – Шахты: Изд-во ЮРГУЭС, 2006.
3. Л.С. Шихобалов О направленности времени.,
Сб. Проблема времени в культуре, философии и науке: сб. науч. тр. / под ред. В.С. Чуракова. (Библиотека времени. Вып. 3). – Шахты: Изд-во ЮРГУЭС, 2006.
4. Р. ди Бартини «Соотношения между физическими величинами» Докл. АН СССР, 163, №4, 1965.; Р. ди Бартини «Соотношения между физическими величинами»// «Проблемы теории гравитации и элементарных частиц». Сб. под ред. д.т.н. К. Станюковича и к.т.н. Г. Горелика. М., Атомиздат, 1966 г., стр. 249-266.
5. Рукопись Р.О. ди Бартини, П.Г. Кузнецов «Множественность геометрий и множественность физик», Материалы семинара «Кибернетика электроэнергетических систем». Брянск, 1974.
6. Роберт Орос ди Бартини.,- Советский авиаконструктор, физик-теоретик, философ., Статьи по физике и философии,, Москва 2009, редакция журнала «Самообразование»,
урл]хттпс://docs.google.com/uc?id=0B9f0hkLDRDvROTNPR3dNWFJTZ3kyV21JLUlwYmktUQ&export=download/урл]
7. Мельников Г.С., Ошарин А.А., Андреева О.В., Кушнаренко А.П Нано-синтез фотонных кристаллов и фрактальных структур в объемных высокоразрешающих регистрирующих средах. ( Обзоры) Урл]хттп://www.nanometer.ru/2008/06/29/cgh_53362.html/Урл]
и
Url]http://ввв.нанометер.ру/2008/06/29/цгх_53362/ПРОП_ФИЛЕ_филес_1/МЕТМАТ_ОПТИЦС.пдф/Урл],
8. А.Е. Петров Тензорный метод двойственных сетей ,/А.Е. Петров – М.: ООО «Центр информационных технологий в природопользовании» , Москва 2007г. – 496 с.:
http://сапр.мсму.ру/лецтматериалс/тмдц.пдф /Урл] <...рл]хттп://files.mail.ru/20V37H
по состоянию на 26.10.2012
ПРИЛОЖЕНИЕ №1

/img0.liveinternet.ru/images/attach/c/5/84/920/84920046_20120318_i_j_k.gif"">
/img1.liveinternet.ru/images/attach/c/2//72/132/72132254_Bifinsl_bitetr.png"">

Улыбнитесь - 1

 

Давайте улыбнёмся!

Серия сообщений "Котоматрица":
Часть 1 - Улыбнитесь - 4
Часть 2 - Улыбнитесь - 3
...
Часть 7 - Забавный котёнок!
Часть 8 - Гламурно жить не запретишь (кошки)!
Часть 9 - Улыбнитесь - 1

Ответы Константина.

В силу того, что предыдущее письмо ВЧ касалось прямых рекомендаций Вадима Константину по технике прохождения этапа получения прибамбаса дфмн я из него выделю только краткую квинт. эссенцию:Крысис и зания о пространсве энд времени-вещи принципиально разные, как котлеты и мухи либо -как мухи с котлетами-по разные стороны баррикад.
...Если К.-житель Московии или Подмосковья -то ему крайне желательно походить по вторникам вечером на Биофак МГУ на семинары по времени А.П.Левича-может быть даже примкнуть к семинаристам Левича, стать одним из них.... Само письмо Вадима достаточно объемное, по этому ответы Кости, так же приведу выборочно:

Константин:
Геннадий Семенович, здравствуйте!

Благодарю за информирование о мнении Вадима - здесь есть что учитывать в своей работе.
Я позволю себе здесь попробовать оспорить ряд тезисов, которые вводит уважаемый Вадим.
Во-первых, я не согласен, что наши знания о пространстве-времени не влияют на современное состояние экономики.
Здесь я рисую для себя следующую цепочку. Нет прорывных фундаментальных исследований (знаний о пространстве-времени) - нет прорывных технологий (не на чем строить прикладные технологии) - нет масштабных инвестиций в инновационную сферу (на сегодня ни биотехнологии, ни нанотехнологии не готовы принять на себя инвестиции размером в десятки и сотни миллиардов долларов). Фактически инвесторам просто некуда вкладывать деньги. Деньги простаивают. Жизненный цикл научно-технической революции затягивается. Все уповают на то, что де фундаментальные исследования долго переходят в прикладные разработки и делают на этом "объективную" теорию (например, циклы Шумпетера), что частично оправданно, но не решает в корне проблему. Таким образом, из-за отсутствия глубоких знаний о пространстве-времени и как следствие прорывных технологий затормаживается развитие экономики.
Во-вторых, я не согласен, что нужно слепо ориентироваться на классиков в экономике, например, Маркс. У меня созрела некоторая критика, которую я бы тоже хотел Вам представить по случаю. В современной экономической теории время возведено в разряд абсолютных и незыблемых элементов фундамента теории, что безусловно верно, но не очень точно. Так мы учитываем общественно необходимое время, но не учитываем откуда оно берется и куда оно пропадает. В теории систем и в экономической науке отсутствует подробное рассмотрение категории внимания человека, как измеримой величины. Я представляю себе, что внимание человека непрерывно генерируется и расходуется в процессе жизни человека. Внимание опосредует всю жизнь человека: его движения, его мысли, его слова, наблюдение за окружением - всё опосредуется вниманием человека.
Здесь необходимо вводить понятие о внимании системы. Внешняя информационная среда - внимание - внутренняя информационная среда - принятие решения - действие во внешней среде. Вот, например, информация с печатного документа должна попасть в базу данных на компьютер. Её надо либо набрать на компьютере через клавиатуру, либо ввести с помощью сканера. Это и будет операция по введение во внимание системы-компьютера информации. Скорость внимания - это то сколько времени требуется для попадания из внешней информационной среды во внутреннюю информационную среду системы. Объем внимания измерим с помощью меры Л+Т+, например, м*с (метро-секунды), или м8*с8. Скорость внимания выразима с помощью меры Л-Т+ с/м - сколько секунд нужно для "оцифровки" одного метра во внутреннюю информационную среду системы - та временная задержка которая возникает у времени на пути внутрь системы.
Соответственно, когда мы создаем иной базис для осмысления экономических процессов, то и вся экономика предстает перед нами в ином свете. Вся экономика, все экономические процессы, могут быть рассмотрены как непрерывные преобразования в пространстве-времени. Организации и организмы - это преобразователи пространства-времени различного типа. Так за счет правильно подобранных масштабов деятельности каждая организация (от отдельного существа и человека, до страны и цивилизации в целом) выполняет преобразование время-пространство-время*, что и создает экономию общественного времени и уже потом тянет за собой преобразование деньги-товар-деньги*. Таким образом, в процессе нашей работы прежде всего мы работаем нашим вниманием. От того как наше внимание распределяется зависит та эффективность, которую мы получаем от деятельности - то насколько мы эффективно расходуем (инвестируем) время. Внимание в труде первично, а время - вторично. Знания являются силой еще и потому, что помогают организовывать наше внимание и таким образом ускорять процессы обработки информации и принятия обоснованных решений. Таким образом, необходимо верно распределять внимание организации на всех уровнях: внимание человека, внимание объединения людей, внимание организаций, внимание систем. Политика должна заниматься организацией внимания на разных уровнях: она должна показывать куда внимание привлечь, а откуда его отвлечь.

Думаю, участники переписки не будут на меня в обиде за вольную редакцию (сокращение)

Запретные темы.

Расширение нашего восприятия - есть фундамент нашего развития. Меняется наше восприятие - "меняется вселенная". Для изменения своего восприятия надо заниматься изучением своего восприятии, т.е. самопознанием. "Познай себя - познаешь вселенную" - говорили древние. В чём кризис некоторых аспектов современной науки? В ограниченности восприятия тех учёных, которые занимаются этими аспектами. Что делают мировые правители? Правильно! Ограничивают наше восприятие.

Авиаконструктор Бартини

Гений не от мира сего.

Все историки сходятся в одном: Роберто Бартини – это гений из плеяды Леонардо да Винчи, Джордано Бруно и Галилея – великих учёных. 

Бартини сделал доклад в сентябре 1974 года, в котором он предложил авианосцы на подводных крыльях. На скоростях 600—700 км/час шел авианосец, так что самолет мог садиться без гашения скорости. Когда Бартини сделал свой доклад, то Алексеев из Горького отказался делать свой доклад, сославшись на то, что его доклад хуже.

Яковлев, Александр Сергеевич: «Что это мы тут шумим? У нас же есть Бартини — вот и поручим проблему ему! Уж если он ее не решит, значит, она принципиально нерешаема…»

СМОТРЕТЬ ЕЩЕ ВИДЕО

"Неразрешённые тайны" Клауса Дона!
 

Klaus Dona (КД) - куратор Арт Экспозиции Дома Габсбургов, Австрия. Господин Дона, будучи опытным специалистом в организации художественных выставок по всему миру, оказался свидетелем существования феноменальных археологических находок, не поддающихся объяснениям здравого смысла и классификации в современном историческом контексте. То есть, это артефакты, которые не должны были существовать, в соответствии с современной наукой. Клаус Дона исследовал эти типы артефактов в течение десятилетий, и после долгой и скрупулёзной подготовки, решил представить их в экспозиции, названной "Неразрешённые тайны". В проекте "Авалон" представлены слайды из этой выставки с комментариями самого Дон а Клауса.

Это видео на 45 минут просмотра- слайд-шоу с личными комментариями Клауса Дона.

Чтобы смотреть с субтитрами,нажмите внизу на панели кнопочку СС !!!!!!!!!!

НЛО. Гитлер. База 211 на Антарктиде 1/4
 

Читать далее...

Удивительная музыка Альфреда Шнитке...
 

 
 

The Story of the Unknown Actor

Composer: Alfred Schnittke (1934-1998)
Performer: Berlin Radio Symphony Orchestra
Conductor: Frank Strobel

 

1. Thema - Titelmusik

2. Agitato - Schlitten

3. Agitato - Reise

4. Waltzer (Abschied)

5. Thema und Marsch

6. Epilog

http://poiskm.ru/index.php/get/strack/865a40/ab84c5/f?q=588519819caf46fa2e523f5bfcff4c16&download.mp3

7. Светлая душа

Модель подарка 8 марта



1.


2.


3.


4.


5.


6.


7.


8.


9.


10.


11.


12.

Вселенная Бартини

«... в другом сообщении будет показано, что (3+3)-мерность пространства-времени является экспериментально проверяемым фактом и что шестимерная модель свободна от логических трудностей, созданных (3+1)-мерной концепцией».... (Бартини, 1962 год)

На конференцию THE PHYSICS OF REALITY:
SPACE, TIME, MATTER, COSMOS

FIRST Joint Meeting:
PIRT XIV - VIGIER VIII

готовлю статью "Шестимерный мир Бартини-Пуанкаре". Ваши иллюстрации укладываются в эту модель. С Вашего позволения цитирую.
Геннадий Семёнович.

Технология спаивания [2012]





Просто шикарный документальный фильм, развевающий миф о том что Водка это исконно русский напиток, и что в России всегда бухали.
Один мой хороший друг, после просмотра этого фильма, навсегда бросил пить.

ЧУДО! Геннадий Семёнович <стронг>Моя живопись<бр/><бр/> <п><див стыле="видтх: ауто; хеигхт: ауто; оверфлов: хидден; паддинг: 8пх"><див стыле="паддинг: 16пх; техт-алигн: центер"><а хреф="хттп://www.liveinternet.ru/app/fotograf/index.php?s=photo_viewer&ev=photo_view&uid=3319431&bid=3319431&pid=891401&id=2889609&mode=this" таргет="топ"><имг срц="хттп://img1.liveinternet.ru/images/foto/c/9/apps/2/889/2889609__0266dfaddbd9.jpg" видтх="635" хеигхт="500" стыле="бордер: 0пх; маргин: 0пх; паддинг: 0пх" /><див стыле="техт-алигн: центер; фонт-сизе: 12пх; цолор: #000; паддинг-топ: 4пх">1.&нбсп;more]