-Рубрики
- глобально (212)
- наши дети (74)
- православие (14)
- чипизация (14)
- лирика (6)
- статистика (4)
- протесты, митинги (4)
- психолого-филосовское (2)
- здоровье (96)
- отрава (28)
- травки (16)
- прививки (12)
- образование (62)
- о разном (20)
- притчи, мудрые мысли (4)
- математика (44)
- кружок (19)
- информатика (5)
- высшая (5)
- школьная (3)
- (0)
-Музыка
- Вальс дождя
- Слушали: 134767 Комментарии: 0
-Поиск по дневнику
-Подписка по e-mail
-Статистика
Фракталы |
Фрактал (лат. fractus — дробленый, сломанный, разбитый) — сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.
http://www.newscientist.com/
Серия сообщений "математика":математикаЧасть 1 - числа
Часть 2 - ?? посмотреть симметрия
...
Часть 9 - А ты веришь в закономерности ??????
Часть 10 - Родителям дошкольников рекомендации, советы, презентации, тесты
Часть 11 - Фракталы
Часть 12 - Сакральная геометрия
Часть 13 - Экстрасенсорика: Энергоинформационное поле Вселенной - все события на Земле сохраняются вечно
...
Часть 39 - Музыка сфер Пифагора
Часть 40 - Учебники
Часть 41 - Нечеткая логика
| Рубрики: | математика/кружок |
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |

Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature'. В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.
Роль фракталов в машинной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.
Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале. Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому".
Существует большое число математических объектов называемых фракталами (треугольник Серпинского, снежинка Коха, кривая Пеано, множество Мандельброта и лоренцевы аттракторы). Фракталы с большой точностью описывают многие физические явления и образования реального мира: горы, облака, турбулентные (вихревые) течения, корни, ветви и листья деревьев, кровеносные сосуды, что далеко не соответствует простым геометрическим фигурам. Впервые о фрактальной природе нашего мира заговорил Бенуа Мандельброт в своей основополагающей работе "Фрактальная геометрия природы" .
Термин фрактал введен Бенуа Мандельбротом в 1977 году в его фундаментальной работе "Фракталы, Форма, Хаос и Размерность" . Согласно Мандельброту, слово фрактал происходит от латинских слов fractus - дробный и frangere - ломать, что отражает суть фрактала, как "изломанного", нерегулярного множества .
Классификация фракталов.
Для того, чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации. Существует три класса фракталов.
1. Геометрические фракталы.
Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор в соответствующем масштабе. В результате бесконечного повторения этой процедуры получается геометрический фрактал.
Рассмотрим на примере один из таких фрактальных объектов – триадную кривую Коха.
Построение триадной кривой Коха.
Возьмем прямолинейный отрезок длины 1. Назовем его затравкой. Разобьем затравку на три равные части длиной в 1/3, отбросим среднюю часть и заменим ее ломаной из двух звеньев длиной 1/3.
Мы получим ломаную, состоящую из 4 звеньев с общей длиной 4/3 , - так называем первое поколение.
Для того чтобы перейти к следующему поколению кривой Коха, надо у каждого звена отбросить и заменить среднюю часть. Соответственно длина второго поколения будет 16/9, третьего – 64/27. если продолжить этот процесс до бесконечности, то в результате получится триадная кривая Коха.
Рассмотрим теперь св-ва триадной кривой Коха и выясним, почему же фракталы называли «монстрами».
Во-первых, эта кривая не имеет длины – как мы убедились, с числом поколений ее длина стремится к бесконечности.
Во-вторых, к этой кривой невозможно построить касательную – каждая ее точка является точкой перегиба, в которой производная не существует, - эта кривая не гладкая.
Длина и гладкость – фундаментальные св-ва кривых, которые изучаются как евклидовой геометрией, так и геометрией Лобачевского, Римана. К триадной кривой Коха традиционные методы геометрического анализа оказались неприменимы, поэтому кривая Коха оказалась чудовищем – «монстром» среди гладких обитателей традиционных геометрий.
Построение "дракона" Хартера-Хейтуэя.

Для получения другого фрактального объекта нужно изменить правила построения. Пусть образующим элементом будут два равных отрезка, соединенных под прямым углом. В нулевом поколении заменим единичный отрезок на этот образующий элемент так, чтобы угол был сверху. Можно сказать, что при такой замене происходит смещение середины звена. При построении следующих поколений выполняется правило: самое первое слева звено заменяется на образующий элемент так, чтобы середина звена смещалась влево от направления движения, а при замене следующих звеньев, направления смещения середин отрезков должны чередоваться. На рисунке представлены несколько первых поколений и 11-е поколение кривой, построенной по вышеописанному принципу. Кривая, при n стремящемуся к бесконечности, называется драконом Хартера-Хейтуэя.
В машинной графике использование геометрических фракталов необходимо при получении изображений деревьев, кустов. Двухмерные геометрические фракталы используются для создания объемных текстур (рисунка на поверхности объекта).
2.Алгебраические фракталы
Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоваться терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.
Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.
Множество Мандельброта. 
В качестве примера рассмотрим множество Мандельброта. Алгоритм его построения достаточно прост и основан на простом итеративном выражении: Z[i+1] = Z[i] * Z[i] + C, где Zi и C - комплексные переменные. Итерации выполняются для каждой стартовой точки с прямоугольной или квадратной области - подмножестве комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0), (это означает, что аттрактор динамической системы находится в бесконечности), или после достаточно большого числа итераций (например 200-500) Z[i] сойдется к какой-нибудь точке окружности. В зависимости от количества итераций, в течении которых Z[i] оставалась внутри окружности, можно установить цвет точки C (если Z[i] остается внутри окружности в течение достаточно большого количества итераций, итерационный процесс прекращается и эта точка растра окрашивается в черный цвет).
3.Стохастические фракталы
Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе хаотически менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря .
Существуют и другие классификации фракталов, например деление фракталов на детерминированные (алгебраические и геометрические) и недетерминированные (стохастические).
О применении фракталов
Прежде всего, фракталы - область удивительного математического искусства, когда с помощью простейших формул и алгоритмов получаются картины необычайной красоты и сложности! В контурах построенных изображений нередко угадываются листья, деревья и цветы.
Одни из наиболее мощных приложений фракталов лежат в компьютерной графике. Во-первых, это фрактальное сжатие изображений, и во-вторых построение ландшафтов, деревьев, растений и генерирование фрактальных текстур. Современная физика и механика только-только начинают изучать поведение фрактальных объектов. И, конечно же, фракталы применяются непосредственно в самой математике.
Достоинства алгоритмов фрактального сжатия изображений - очень маленький размер упакованного файла и малое время восстановления картинки. Фрактально упакованные картинки можно масштабировать без появления пикселизации. Но процесс сжатия занимает продолжительное время и иногда длится часами. Алгоритм фрактальной упаковки с потерей качества позволяет задать степень сжатия, аналогично формату jpeg. В основе алгоритма лежит поиск больших кусков изображения подобных некоторым маленьким кусочкам. И в выходной файл записывается только какой кусочек какому подобен. При сжатии обычно используют квадратную сетку (кусочки - квадраты), что приводит к небольшой угловатости при восстановлении картинки, шестиугольная сетка лишена такого недостатка.
Компанией Iterated разработан новый формат изображений "Sting", сочетающий в себе фрактальное и «волновое» (такое как в формате jpeg) сжатие без потерь. Новый формат позволяет создавать изображения с возможностью последующего высококачественного масштабирования, причем объем графических файлов составляет 15-20% от объема несжатых изображений.
Склонность фракталов походить на горы, цветы и деревья эксплуатируется некоторыми графическими редакторами, например фрактальные облака из 3D studio MAX, фрактальные горы в World Builder. Фрактальные деревья, горы и целые пейзажи задаются простыми формулами, легко программируются и не распадаются на отдельные треугольники и кубики при приближении.
Нельзя обойти стороной и применения фракталов в самой математике. В теории множеств множество Кантора доказывает существование совершенных нигде не плотных множеств, в теории меры самоаффинная функция "Канторова лестница" является хорошим примером функции распределения сингулярной меры.
В механике и физике фракталы используются благодаря уникальному свойству повторять очертания многих объектов природы. Фракталы позволяют приближать деревья, горные поверхности и трещины с более высокой точностью, чем приближения наборами отрезков или многоугольников (при том же объеме хранимых данных). Фрактальные модели, как и природные объекты, обладают "шероховатостью", и свойство это сохраняется при сколь угодно большом увеличении модели. Наличие на фракталах равномерной меры, позволяет применять интегрирование, теорию потенциала, использовать их вместо стандартных объектов в уже исследованных уравнениях.
При фрактальном подходе хаос перестает быть синимом беспорядка и обретает тонкую структуру. Фрактальная наука еще очень молода, и ей предстоит большое будущее. Красота фракталов далеко не исчерпана и еще подарит нам немало шедевров - тех, которые услаждают глаз, и тех, которые доставляют истинное наслаждение разуму.
О построении фракталов
Метод последовательных приближений

Глядя на эту картинку, нетрудно понять, как можно построить самоподобный фрактал (в данном случае пирамиду Серпинского). Нужно взять обычную пирамиду (тетраэдр), затем вырезать ее середину (октаэдр), в результате чего у нас получается четыре маленьких пирамидки. С каждой из них мы проделываем ту же самую операцию и т.д. Это несколько наивное, но наглядное объяснение.
Рассмотрим суть метода более строго. Пусть имеется некоторая IFS-система, т.е. система сжимающих отображений S={S1,...,Sm} Si:Rn->Rn (например, для нашей пирамидки отображения имеют вид Si(x)=1/2*x+oi, где oi - вершины тетраэдра, i=1,..,4). Затем выбираем некоторое компактное множество A1 в Rn (в нашем случае выбираем тетраэдр). И определяем по индукции последовательность множеств Ak:Ak+1=S1(Ak) U...U Sm(Ak). Известно, что множества Ak с ростом k, всё лучше приближают искомый аттрактор системы S.
Заметим, что каждая из этих итераций является аттрактором рекуррентной системы итерированных функций (английский термин Digraph IFS, RIFS и также Graph-directed IFS) и поэтому их легко построить с помощью нашей программы.
Построение по точкам или вероятностный метод
Это наиболее лёгкий для реализации на компьютере метод. Для простоты рассмотрим случай плоского самоаффинного множества. Итак, пусть {S
1
,..,S
m
} - некоторая система аффинных сжатий. Отображения S
i
представимые в виде: S
i
(x)=A
i
( x-o
i
)+o
i
, где A
i
- фиксированная матрица размера 2x2 и o
i
- двумерный вектор столбец.
- Возьмем неподвижную точку первого отображения S1 в качестве начальной точки:
x := o1;
Здесь мы пользуемся тем, что все неподвижные точки сжатий S1,..,Sm принадлежат фракталу. В качестве начальной точки можно выбрать произвольную точку и порожденная ею последовательность точек стянется к фракталу, но тогда на экране появятся несколько лишних точек. - Отметим текущую точку x=(x1,x2) на экране:
putpixel(x1,x2,15); - Выберем случайным образом число j от 1 до m и пересчитаем координаты точки x:
j:=Random(m)+1;
x:=Sj(x); - Переходим на шаг 2, либо, если сделали достаточно большое число итераций, то останавливаемся.
Примечание. Если коэффициенты сжатия отображений Si разные, то фрактал будет заполняться точками неравномерно. В случае, если отображения Si являются подобиями, этого можно избежать небольшим усложнением алгоритма. Для этого на 3-ем шаге алгоритма число j от 1 до m надо выбирать с вероятностями p1=r1s,..,pm=rms, где ri обозначают коэффициенты сжатия отображений Si, а число s (называемое размерностью подобия) находится из уравнения r1s+...+rms=1. Решение этого уравнения можно найти, например, методом Ньютона.
О фракталах и их алгоритмах
Фрактал происходит от латинского прилагательного "fractus", и в переводе означает состоящий из фрагментов, а соответствующий латинский глагол "frangere" означает разбивать, то есть создавать неправильные фрагменты. Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Термин был предложен Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта «The Fractal Geometry of Nature» - «Фрактальная геометрия природы». В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф).
Коррективы
Позволю себе внести некоторые коррективы в алгоритмы предложенные в книге Х.-О. Пайтгена и П.Х.Рихтера "Красота фракталов" М. 1993 сугубо для искоренения опечаток иоблегчения понимания процессов поскольку после их изучения многое осталось для меня загадкой. К сожалению эти "понятные" и "простые" алгоритмы ведут качующий образ жизни.
В основе построения фракталов лежит некая нелинейная функция комплексного процесса с обратной связью z=> z2+c поскольку z и с -комплексные числа, то z=x+iy, c=p+iq необходимо разложить его на х и у чтобы перейти в более реальную для простого человека плоскость:
x(k+1)=x(k)2-y(k)2 + p,
y(k+1)=2*x(k)*y(k) + q.
Плоскость, состоящая из всех пар (x,y), может рассматриваться, как при фиксированных значениях р и q, так и при динамических. В первом случае перебирая по закону все точки (х,у) плоскости и окрашивая их в зависимости от количества повторений функции необходимых для выхода из итерационного процесса или не окрашивая (черный цвет) при привышении допустимого максимума повторений мы получим отображение множества Жюлиа. Если, напротив, определить начальнуюя пару значений (x,y) и проследить ее колористическую судьбу при динамически изменяющихся значениях параметров p и q, то получаим изображения, называемые множествами Мандельброта.
Это только присказка и дальше по порядку.
К вопросу об алгоритмах раскраски фракталов.
Обычно тело множества представляют в виде черного поля, хотя очевидно, что черный цвет может быть заменен на любой другой, но это тоже мало интересный результат. Получить изображение множества раскрашенного во все цвета - задача которая не может решаться при помощи циклических операций т.к. количество итерации формирующих тело множества равно максимально возможному и всегда одно и тоже. Раскрасить множество в разные цвета возможно применив в качестве номера цвета результат проверки условия выхода из цикла ( z_magnitude) или подобный ему, но с другими математическими действиями.
Применение "фрактального микроскопа"
для демонстрации пограничных явлений.
Аттракторы - центры ведущие борьбу за доминирование на плоскости. Между аттракторами возникает граница представляющая витееватый узор. Увеличивая масштаб рассмотрения в пределах границ множества можно получать нетривиальные узоры отражаюшие состояние детерминированного хаоса - обычного явления в мире природы.
Исследуемые географами объекты образуют систему с весьма сложно организованными границами, в связи с чем их проведение становится не простой практической задачей. Природные комплексы имеют ядра типичности выступающие в качестве аттракторов теряющих силу влияния на территорию по мере ее удаления.
Используя фрактальный микроскоп для множеств Мандельброта и Жюлиа можно сформировать представление о пограничных процессах и явлениях, одинаково сложных не зависимо от масштаба рассмотрения и таким образом подготовить восприятие специалиста к встрече с динамичным и на первый взгляд хаотичным в пространстве и времени природным объектом, к пониманию фрактальной геометрии природы. Многоцветие красок и фрактальная музыка определенно оставят глубокий след в сознании учащихся.
Фракталам посвящены тысячи публикаций и огромные ресурсы интернет, однако для многих специалистов далеких от информатики данный термин представляется абсолютно новым. Фракталы, как объекты представляющие интерес для специалистов различных отраслей знания, должны получить надлежащее место в курсе информатики.
Примеры
| РЕШЕТКА СЕРПИНСКОГО |
 Это один из фракталов, с которыми экспериментировал Мандельброт, когда разрабатывал концепции фрактальных размерностей и итераций. Треугольники, сформированные соединением средних точек большего треугольника вырезаны из главного треугольника, образовывая треугольник, с большим количеством дырочек. В этом случае инициатор - большой треугольник а шаблон - операция вырезания треугольников, подобных большему. Так же можно получить и трехмерную версию треугольника, используя обыкновенный тетраэдр и вырезая маленькие тетраэдры. Размерность такого фрактала ln3/ln2 = 1.584962501. Чтобы получить ковер Серпинского, возьмем квадрат, разделим его на девять квадратов, а средний вырежем. То же сделаем и с остальными, меньшими квадратами. В конце концов образуется плоская фрактальная сетка, не имеющая площади, но с бесконечными связями. В своей пространственной форме, губка Серпинского преобразуется в систему сквозных форм, в которой каждый сквозной элемент постоянно заменяется себе подобным. Эта структура очень похожа на разрез костной ткани. Когда-нибудь такие повторяющиеся структуры станут элементом строительных конструкций. Их статика и динамика, считает Мандельброт, заслуживает пристального изучения. |
| ФРАКТАЛ СЕРПИНСКОГО |
 Не перепутайте этот фрактал с решеткой Серпинского. Это два абсолютно разных объекта. В этом фрактале, инициатор и генератор одинаковы. При каждой итерации, добавляется уменьшенная копия инициатора к каждому углу генератора и так далее. Если при создании этого фрактала произвести бесконечное число итераций, он бы занял всю плоскость, не оставив ни одной дырочки. Поэтому его фрактальная размерность ln9/ln3 = 2.0. |
| КРИВАЯ КОХА |
 Кривая Коха один из самых типичных детерминированных фракталов. Она была изобретена в девятнадцатом веке немецким математиком по имени Хельге фон Кох, который, изучая работы Георга Контора и Карла Вейерштрассе, натолкнулся на описания некоторых странных кривых с необычным поведением. Инициатор - прямая линия. Генератор - равносторонний треугольник, стороны которого равны трети длины большего отрезка. Эти треугольники добавляются к середине каждого сегмента снова и снова. В своем исследовании, Мандельброт много экспериментировал с кривыми Коха, и получил фигуры такие как Острова Коха, Кресты Коха, Снежинки Коха и даже трехмерные представления кривой Коха, используя тетраэдр и прибавляя меньшие по размерам тетраэдры к каждой его грани. Кривая Коха имеет размерность ln4/ln3 = 1.261859507. |
| ФРАКТАЛ МАНДЕЛЬБРОТА |
 Это НЕ множество Мандельброта, которое можно достаточно часто видеть. Множество Мандельброта основано на нелинейных уравнениях и является комплексным фракталом. Это тоже вариант кривой Коха несмотря на то, что этот объект не похож на нее. Инициатор и генератор так же отличны от использованных для создания фракталов, основанных на принципе кривой Коха, но идея остается той же. Вместо того, чтобы присоединять равносторонние треугольники к отрезку кривой, квадраты присоединяются к квадрату. Благодаря тому, что этот фрактал занимает точно половину отведенного пространства при каждой итерации, он имеет простую фрактальную размерность 3/2 = 1.5. |
| ФРАКТАЛЫ ЗВЕЗДА И СНЕЖИНКА |
 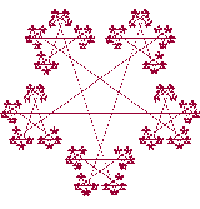 Оба эти объекта не являются классическими фракталами и они не были изобретены Мандельбротом или кем-либо из известных математиков. Я просто создал эти фракталы из интереса и чтобы поэкспериментировать в программировании. И инициатор и генератор здесь фигура, сформированная соединением средних точек сторон со средними точками противолежащих сторон в правильном шестиугольнике. Более того, я могу только подозревать о размерности этих фракталов. |
| ПЯТИУГОЛЬНИК ДАРЕРА |
Фрактал выглядит как связка пятиугольников, сжатых вместе. Фактически он образован при использовании пятиугольника в качестве инициатора и равнобедренных треугольников, отношение большей стороны к меньшей в которых в точности равно так называемой золотой пропорции (1.618033989 или 1/(2cos72)) в качестве генератора. Эти треугольники вырезаются из середины каждого пятиугольника, в результате чего получается фигура, похожая на 5 маленьких пятиугольников, приклеенных к одному большому. Вариант этого фрактала можно получить при использовании в качестве инициатора шестиугольника. Этот фрактал называется Звезда Давида и он довольно похож на шестиугольную версию Снежинки Коха. Фрактальная размерность пятиугольника Дарера ln6/ln(1+g), где g - отношение длины большей стороны треугольника к длине меньшей. В данном случае, g - это Золотая Пропорция, так что фрактальная размерность приблизительно равна 1.86171596. Фрактальное измерение Звезды Давида ln6/ln3 или 1.630929754. |
| КРИВАЯ ГИЛЬБЕРТА |
 Этот фрактал очень похож на Фрактал Лабиринт, кроме того факта что ширина буквы U, являющейся генератором не изменяется с каждой итерацией. Однако, в отличии от Фрактала Лабиринта, кривая Гильберта также называемая Отелем Гильберта, имеет одно единственное фрактальное измерение, которое точно равно 2.0, так как при бесконечном количестве итераций, он займет всю плоскость. |
| ФРАКТАЛ КОРОБКА |
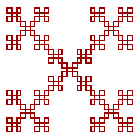 Это очень простой детерминированный фрактал, который образуется при прибавлении квадратов к вершинам других квадратов. И инициатор и генератор - квадраты. Его фрактальная размерность ln8/ln3 или 1.892789261. |
Сложные фракталы
Фактически, если вы увеличите маленькую область любого сложного фрактала а затем проделаете то же самое с маленькой областью этой области, то эти два увеличения будут значительно отличаться друг от друга. Два изображения будут очень похожи в деталях, но они не будут полностью идентичными.
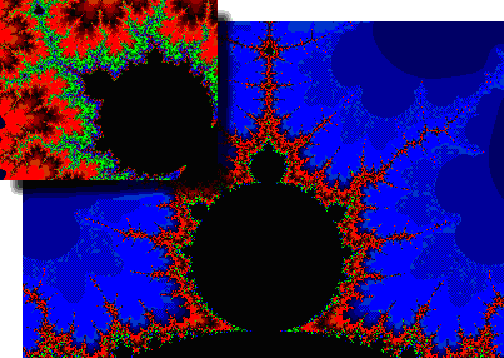 Рис 1. Приближение множества Мандельброта
Рис 1. Приближение множества Мандельброта
Сравните, например приведенные здесь картинки множества Мандельброта, одна из которых получена при увеличении некоторой области другой. Как видно, они абсолютно не являются идентичными, хотя на обоих мы видим черный круг, от которого в разные стороны идут пылающие щупальца. Эти элементы повторяются бесконечно долго во множестве Мандельброта в уменьшающейся пропорции.
Детерминистские фракталы являются линейными, тогда как сложные фракталы таковыми не являются. Будучи нелинейными, эти фракталы генерируются тем, что Мандельброт назвал нелинейными алгебраическими уравнениями. Хороший пример - это процесс Zn+1=ZnІ + C, что является уравнением, используемым для построения множества Мандельброта и Жулии второй степени. Решение этих математических уравнений вовлекает комплексные и мнимые числа. Когда уравнение интерпретируется графически на комплексной плоскости, результатом оказывается странная фигура, в которой прямые линии переходят в кривые, появляются хотя и не без деформаций, эффекты самоподобия на различных масштабных уровнях. При этом вся картина в целом является непредсказуемой и очень хаотичной.
Как можно увидеть, смотря на картинки, сложные фракталы действительно очень сложны и их невозможно создать без помощи компьютера. Для получения красочных результатов этот компьютер должен обладать мощным математическим сопроцессором и монитором с высоким разрешением. В отличии от детерминистских фракталов, сложные фракталы не вычисляются за 5-10 итераций. Практически каждая точка на экране компьютера как отдельный фрактал. Во время математической обработки, каждая точка рассматривается как отдельный рисунок. Каждой точке соответствует определенное значение. Уравнение встраивается, применительно к каждой точке и производится, к примеру 1000 итераций. Для получения сравнительно неискаженного изображения за приемлемый для домашних компьютеров промежуток времени, для одной точки возможно проводить 250 итерации.
Большинство фракталов, которые мы видим сегодня, красиво раскрашены. Возможно фрактальные изображения получили такое большое эстетическое значение именно благодаря своим цветовым схемам. После того, как уравнение посчитано, компьютер анализирует результаты. Если результаты остаются стабильными, или колеблются вокруг определенного значения, точка обычно принимает черный цвет. Если значение на том или ином шаге стремится к бесконечности, точку закрашивают в другой цвет, может быть в синий или красный. Во время этого процесса, компьютер назначает цвета для всех скоростей движения.
Обычно, быстро движущиеся точки закрашивают в красный цвет, тогда как более медленные в желтый и так далее. Темные точки, вероятно, самые стабильные.
Сложные фракталы отличаются от детерминистских в том смысле, что они бесконечно сложные, но, при этом, могут быть сгенерированы очень простой формулой. Детерминистским фракталам не нужны формулы или уравнения. Просто возьмите чертежную бумагу и вы можете построить решето Серпинского до 3 или 4 итерации без каких-либо затруднений. Попробуйте сделать это с множеством Жулиа! Легче пойти мерить длину береговой линии Англии!
МНОЖЕСТВО МАНДЕЛЬБРОТА
 Рис 2. Множество Мандельброта
Рис 2. Множество Мандельброта
Множества Мандельброта и Жулиа, вероятно, два наиболее распространенных среди сложных фракталов. Их можно найти во многих научных журналах, обложках книг, открытках, и в компьютерных хранителях экрана. Множество Мандельброта, которое было построено Бенуа Мандельбротом, наверное первая ассоциация, возникающая у людей, когда они слышат слово фрактал. Этот фрактал, напоминающий чесальную машину с прикрепленными к ней пылающими древовидными и круглыми областями, генерируется простой формулой Zn+1=Zna+C, где Z и C - комплексные числа и а - положительное число.
Множество Мандельброта, которое чаще всего можно увидеть - это множество Мандельброта 2й степени, то есть а=2. Тот факт, что множество Мандельброта не только Zn+1=ZnІ+C, а фрактал, показатель в формуле которого может быть любым положительным числом ввел в заблуждение многих. На этой странице вы видите пример множества Мандельброта для различных значений показателя а. 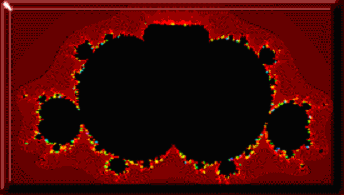
Рис 3. Появление пузырьков при a=3.5
Также популярен процесс Z=Z*tg(Z+C). Благодаря включению функции тангенса, получается множество Мандельброта, окруженное областью, напоминающей яблоко. При использовании функции косинуса, получаются эффекты воздушных пузырьков. Короче говоря, существует бесконечное количество способов настройки множества Мандельброта для получения различных красивых картинок.
МНОЖЕСТВО ЖУЛИА
Удивительно, но множества Жулиа образуются по той же самой формуле, что и множество Мандельброта. Множество Жулиа было изобретено французским математиком Гастоном Жулиа, по имени которого и было названо множество. Первый вопрос, возникающий после визуального знакомства с множествами Мандельброта и Жулиа это "если оба фрактала сгенерированы по одной формуле, почему они такие разные?" Сначала посмотрите на картинки множества Жулиа. Достаточно странно, но существуют разные типы множеств Жулиа. При рисовании фрактала с использованием различных начальных точек (чтобы начать процесс итераций), генерируются различные изображения. Это применимо только ко множеству Жулиа. 
Рис 4. Множество Жулиа
Хотя это нельзя увидеть на картинке, фрактал Мандельброта - это, на самом деле, множество фракталов Жулиа, соединенных вместе. Каждая точка (или координата) множества Мандельброта соответствует фракталу Жулиа. Множества Жулиа можно сгенерировать используя эти точки в качестве начальных значений в уравнении Z=ZІ+C. Но это не значит, что если выбрать точку на фрактале Мандельброта и увеличить ее, можно получить фрактал Жулиа. Эти две точки идентичны, но только в математическом смысле. Если взять эту точку и просчитать ее по данной формуле, можно получить фрактал Жулиа, соответствующий определенной точке фрактала Мандельброта.
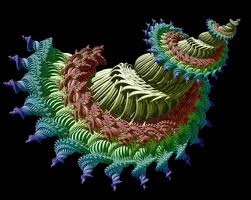

Очень моден нынче термин – фрактал, фрактальность, в смысл которого, как правило, вкладывается принцип самоподобия, т.е. это когда часть\части некого объекта подобна\ы самому объекту. Подробнее (кому это интересно) можете познакомится с материалами в сети Интернет. Одно из не строгих определений фрактала, звучит следующим образом:
Фракталалом называется структура, состоящая из частей, которые в каком-то смысле подобны целому.
Я хочу рассказать о вещах, которые в конце 70 годов мне пришли в голову, и в дальнейшем достаточно основательно изменили мои взгляды и понимание, НА - что такое число, и как следствие, что ЖЪ из себя представляет окружающее пространство. Расскажу, и покажу на примерах как иначе можно интерпретировать натуральные числа? Что они из себя представляют если на них взглянуть в «плоскости самоподобных объектов» - фракталов натуральных чисел.
Человек, в своей жизни, количественно мерит многое. Например, длину пройденного или предстоящего пути, площадь собственного дачного участка, или чужие гектары полей, объем выпитой жидкости или кубометры сваленного мусора. В результате измерений\вычислений итогом служит как правило число. Хотя бывает и «много» или «мало», т.е. результат не в виде числа. Рассмотрим отрезок прямой линии состоящий из 5 одинаковых отрезков.

Если красный отрезок, являющийся частью заданного отрезка увеличить в пять раз или пять раз сложить его с самим собой вдоль прямой, то в результате получится заданный отрезок. Будем считать, что красный отрезок подобен заданному отрезку с коэффициентом подобия равным 5. Исходный отрезок самомподобен, т.е. состоит из частей подобных исходному отрезку. Это соответствует следующей записи в математическом виде:
N = 5*a
где N и a – числа.
Пусть, согласно некоторых соображений у нас получилось, что N = 15.
Если рассматривать в общем случае, а не конкретно данный пример с отрезком, то не важно, о чём оно это число говорит. Просто 15 и всё. Посмотрим можно ли к этому числу применить принцип самоподобия. Если некий целостный объект, состоит из частей, которые ему подобны, то он умещается в этот объект полностью несколько раз. Как например квадратик со стороной равное 1 умещается в квадратик со стороной равной 2 - 4 раза. Количество раз, которое часть умещается в целом, число строго натуральное. Число 15 имеет два сомножителя 3 и 5. При произведении которых, выполняется равенство:
15 = 3*5
Нам из школы известно, что неважно как записать, 3 умножить на 5 или 5 умножить на 3, результат один и тот же, т.е. справедливо равенство:
3*5=5*3
В аксиоматическом поле, данная запись справедлива на основании закона коммутативности.
Если число 15 имеет 5 одинаковых составных частей, то характеристикой его части будет число 3. Если число 15 имеет 3 одинаковых составных части, то характеристикой его части в этом случае будет число 5. Такое рассуждение приводит к следующим выводам:
1.Если 15 состоит из 5 частей то 3 тождественно 15
2.Если 15 состоит из 3 частей то 5 тождественно 15
В данном случае закон коммутативности не совсем очевиден, хотя результат одинаковый, так как смысл вкладываемый в сомножители разный. Если позиционировать данную запись, допустим, первым пишется число раз, а вторым характеризующие число исходного подобия, то закон коммутативности не выполняется, т.е. 3*5 не равно 5*3.
Рассмотрим 1 вывод, так как в нашем примере с отрезком исходное подобие 3 укладывается в исходный объект 5 раз. Зададимся следующим вопросом: Если часть подобна целому, то может часть так же состоит из подобных частей? Допустим да. Тогда исходным объектом уже служит, число 3, а исходным подобием некое число a(1), тогда будет справедлива следующая запись:
3 = 5*a(1)
где а(1) есть числовая характеристика исходного подобия , из которой состоит объект характеризующийся числом 3. Коэффициент подобия остаётся прежним, тем самым сохраняется структурное формирование целого.
Примечание:
Большое в малом и малое в большом! или Большое подобно малому, так же как и малое подобно большому!.
Продолжим процесс далее:
а(1) = 5*а(2)
а(2 )= 5*а(3)
В общем виде это будет выглядеть следующим образом:
а(n) = 5*a(n+1)
a(n+1) = 5*a(n+2)
Если в этих равенствах сделать замену a(n+1) на его значение, определяемое на последующем шаге, то получим следующее равенство:
3=5^n*a(n)
Заменим характеризующее число исходного подобия 3, на отношение N/5. Получим равенство, в котором исключены характеристические числа исходного подобия.
N/5 = 5^n*a(n) или N = 5^(n+1)*a(n).
В этом равенстве n+1 – обозначим, через r (n + 1 = r или n = r - 1). Это натуральное число, говорящее нам о том сколько раз часть исходный самоподобный объект 15 разбивался на подобные части. Из последнего равенства можно определить характеризующее число a(r-1) как:
a(r-1) = N/5^r.
Для первых трёх значений r = {1, 2, 3} будут числа:
a(0) = 3, a(1) = 15/25 = 3/5, a(2) = 15/125 = 3/25
В качестве результата получили рациональные дроби, для которых справедлива запись:
3/25 -> 3/5 -> 3 -> 15
Т.е. все эти числа тождественны, если они укладывались на каждом этапе формируя самоподобные объекты с коэффициентом подобия равным 5.
Представим такой мир, в котором характеризующие числа неких «элементарных» частей всегда равны 1. А далее они неделимы! Допустим единичный отрезок, единичная площадь, единичный электрический заряд. Из этих единичных объектов по определённым правилам строятся более сложные, самоподобные (фрактальные) объекты. В рассматриваем мною, случае это означает, что a(n-1) = 1. Т.е. существует такой этап разбиения самоподобного объекта, при котором мы дошли до единичного размера, который далее неделим. Самоподобие закончилось! Нам необходимо найти r. Определяется оно в нашем примере из равенства:
1 = N/5^r, как r = ln(N)/ln(5) =1.682606195 , где ln – натуральный логарифм.
Что же это получается в результате? Вроде r должно быть число натуральное, а получилось не натуральное. Как понимать не целое количество этапов разбиения самоподобного объекта на подобные части? На этот вопрос я нашёл ответ, но об этом расскажу как-нибудь попозже. В классической теории фракталов, r – определяется как размерность меры.
Если рассмотреть вывод 2, то r будет равно:
1 = 15/3^r, как r = ln(15)/ln(3) = 2.46497352…
В общем случае, если задано некое натуральное число N = k*Y, где k - коэффициент подобия, то справедливо для классического определения в теории фракталов «размерности меры» следующее равенство:
r = ln(N)/ln(k)
Для простых чисел (3, 5, 7, 11 и т.д.) n = 0, т.е. простое число как объект - так же прост, его исходное подобие равно 1.
В качестве ещё одного примера приведу число 231, которое в качестве натуральных сомножителей имеет числа 3, 7, 11.
В этом случае в качестве коэффициентов подобия могут служить уже не два числа, как в верхнем примере, а 6 чисел:
k1 = 3
Y1 = 77 – подобие так же является самоподобным объектом
k2 = 7
Y2 = 33 – подобие так же является самоподобным объектом
k3 = 11
Y3 = 21 – подобие так же является самоподобным объектом
k4 = 3*7 = 21, Y4 = 11
k5 = 3*11 = 33, Y5 = 7
k6 = 7*11 = 77, Y6 = 3
Для этих вариантов «размерность меры» будут следующие:
r1 = ln(231)/ln(3) = 4.953902087
r2 = ln(231)/ln(7) = 2.79684944
r3 = ln(231)/ln(11) = 2.269664473
r4 = ln(231)/ln(21) = 1.787609657
r5 = ln(231)/ln(33) = 1.556529656
r6 = ln(231)/ln(77) = 1.25291471
Продолжение следует
Серия сообщений "Математика":
Часть 1 - Число Пи
Часть 2 - Греко-латинский квадрат
...
Часть 4 - Системы исчисления
Часть 5 - Семь раз отмерь – один раз отрежь!
Часть 6 - Фрактальность натуральных чисел
Воображение многих ученых современности будоражат фракталы. Формы снежинок, пламя костра, кровеносно-сосудистая система у человека, очертания гор, границы материков, русла горных рек, береговая линия и многое другое - все это фракталы. Фракталы позволяют визуально представить математическую идею детерминированного хаоса. Главный их принцип - самоподобие: при рассмотрении фракталов через микроскоп с различным увеличением они выглядят примерно одинаково.























 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |
















