Штрих-код треугольника. Это новое в элементарной геометрии! |
В 2000 году математик Г.Александров обнаружил, что любой треугольник имеет свой индивидуальный штрих-код в виде трех параллельных линий. Построение штрих-кода может выполнить любой школьник, но не любому взрослому удастся доказать, что три прямые действительно параллельные. На рисунке показано сказанное: (ссылки: http://traditio.ru/wiki/%D0%A8%D1%82%D1%80%D0%B8%D...%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0 http://dxdy.ru/topic34484-30.html )
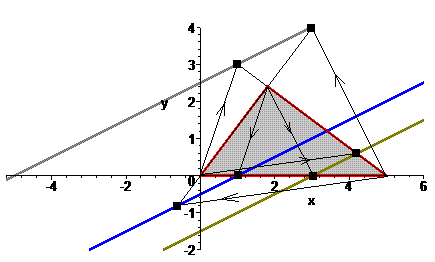
Рис. 1 Построение трех параллельных линий (штрих-кода). Здесь дуги заменены хордами
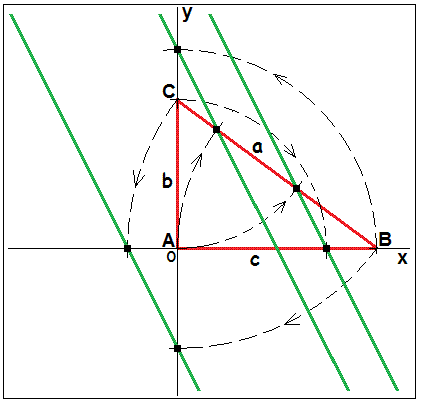
Рис. 2. Построение штрих-кода для прямоугольного треугольника (зеленые прямые) при помощи циркуля и линейки.
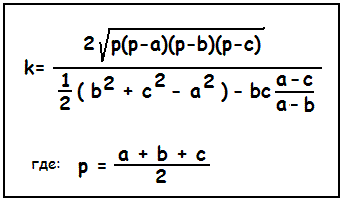
Рис. 3. Коэффициент наклона прямых штрих-кода, полученный из геометрических построений (при условии, что основание треугольника строго гризонтально).

Рис.4. Уравнения прямых штрих-кода. Здесь коэффициент их наклона и другие параметры получены исходя из того, что :
1) вершина А треугольника совпадает с началом координат,
2) основание треугольника лежит на оси ОХ,
3) известна сторона с и координаты вершины С.
Потрясающе интересен график очередности трех линий штрих-кода треугольника в зависимости стороны a от заданных величин сторон b и c . В данном случае b=8 и c=10
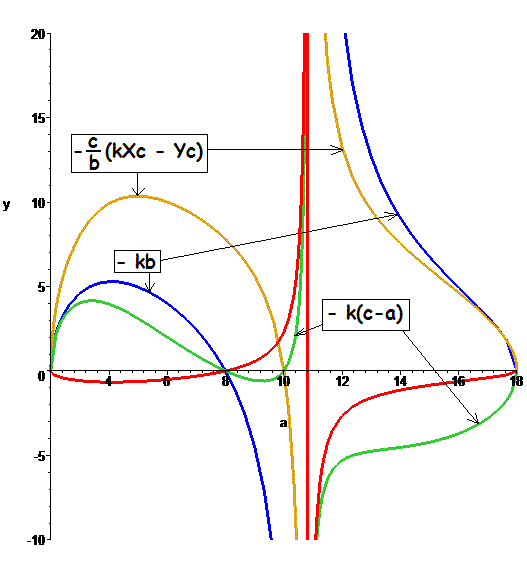
Точка разрыва ao определяется из красивого, но сложного соотношения:
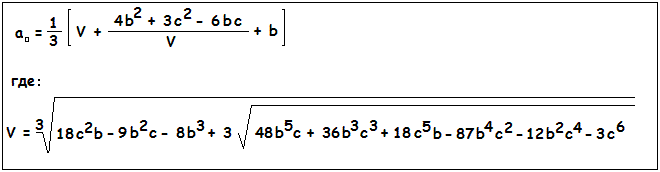
При b=8 ; c=10 значение ao = 10.82651816, что полностью соответствует последнему графику.
Параллельные линии можно использовать и по-иному. Например, две системы по паре параллельных прямых позволяет находить два вида треугольников ABC:
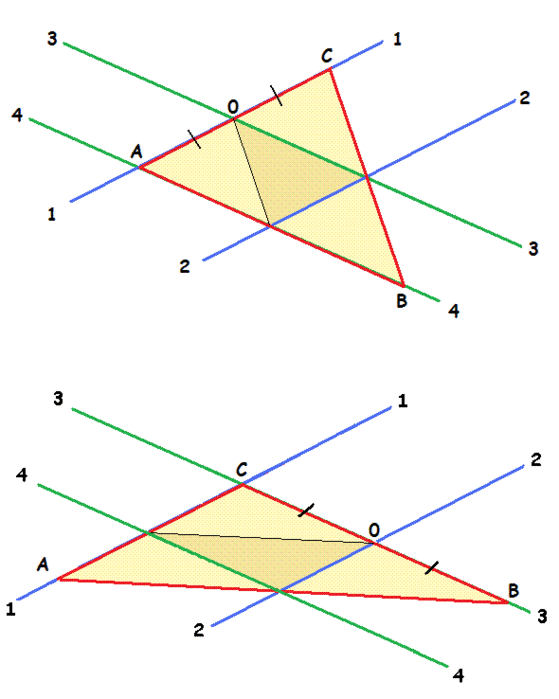
а две системы по три параллельные линии однозначно определяет четырехугольник ABCD:
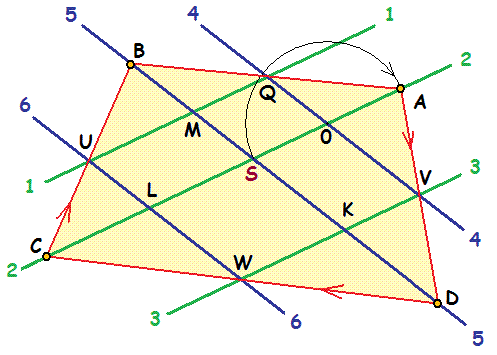

Рис. 1 Построение трех параллельных линий (штрих-кода). Здесь дуги заменены хордами

Рис. 2. Построение штрих-кода для прямоугольного треугольника (зеленые прямые) при помощи циркуля и линейки.
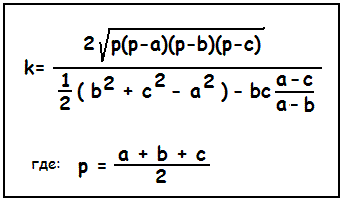
Рис. 3. Коэффициент наклона прямых штрих-кода, полученный из геометрических построений (при условии, что основание треугольника строго гризонтально).

Рис.4. Уравнения прямых штрих-кода. Здесь коэффициент их наклона и другие параметры получены исходя из того, что :
1) вершина А треугольника совпадает с началом координат,
2) основание треугольника лежит на оси ОХ,
3) известна сторона с и координаты вершины С.
Потрясающе интересен график очередности трех линий штрих-кода треугольника в зависимости стороны a от заданных величин сторон b и c . В данном случае b=8 и c=10

Точка разрыва ao определяется из красивого, но сложного соотношения:
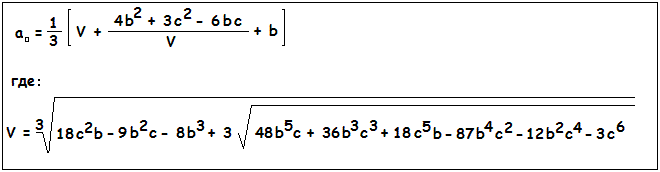
При b=8 ; c=10 значение ao = 10.82651816, что полностью соответствует последнему графику.
Параллельные линии можно использовать и по-иному. Например, две системы по паре параллельных прямых позволяет находить два вида треугольников ABC:

а две системы по три параллельные линии однозначно определяет четырехугольник ABCD:

Процитировано 1 раз
Понравилось: 1 пользователю
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |






