-Рубрики
- квантовая физика (14)
- русский язык (1)
-Метки
-Музыка
- Музыка индейцев Перу:Полёт души
- Слушали: 35155 Комментарии: 0
- Одинокий в ночи
- Слушали: 1213 Комментарии: 2
- ЗАРЯ БАЯЗЕТ.
- Слушали: 329 Комментарии: 0
- Говинда Харе...очень нежное и красивое звучание...
- Слушали: 27194 Комментарии: 0
- По дороге к солнцу. А.Пугачёва.
- Слушали: 940 Комментарии: 6
-Кнопки рейтинга «Яндекс.блоги»
-Подписка по e-mail
-Поиск по дневнику
-Постоянные читатели
---ОЛЯ--- ARINA999 Alina_Serova Annabelle2 Balabka Dardo Firisa GMelnikov ILLANG Lebed_a Leo_Lynxie Lukerija Necky Puppy777 REMEUR Radoprav SPACELilium Savitridevi Semizora Tbor Varasvet alexandre75 erzsi1961 gornjak italija leonarda478 lief mamanyta oksymoron v1_93 vicky_sb АльтэрЭго Асмик Белояна Бивис Волшебник_555 Госпожа_Чу Джанэтт Звон_Рун ИЛ-72 ИРИАНА Лена_Ст Любовь_Шидловская Ниранджани Свирга Худышка_Ла Шёпот_Рун Шмелева_Светлана гагарина макошь311
-Сообщества
Читатель сообществ
(Всего в списке: 1)
КЕТЦАЛЬКОАТЛЬ
-Трансляции
-Статистика
Создан: 30.07.2007
Записей: 1105
Комментариев: 6135
Написано: 13114
Записей: 1105
Комментариев: 6135
Написано: 13114
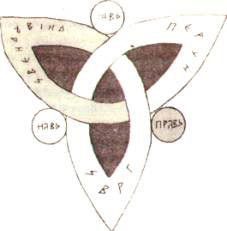
Древний славянский символ Триглав и современная схема геометрии пространства. |
Похожи очень.
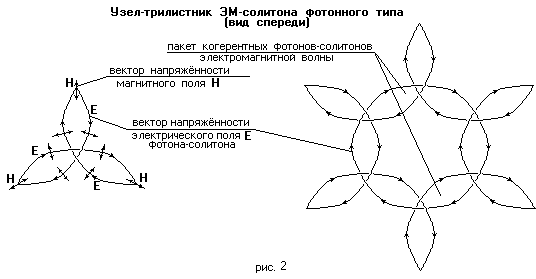
Ранее из моих художеств о понимании сути меркабы (здесь те же круги только закрученные по три в разные стороны. А если все их по часовой крутить то и получится схемка математиков что самая первая, вверху..
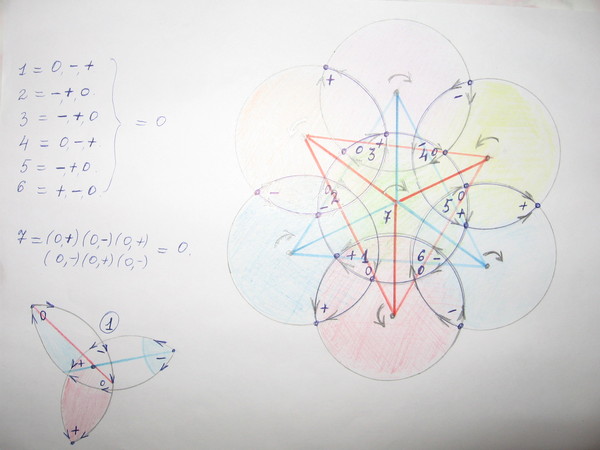


Ранее из моих художеств о понимании сути меркабы (здесь те же круги только закрученные по три в разные стороны. А если все их по часовой крутить то и получится схемка математиков что самая первая, вверху..

Процитировано 5 раз
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |
Аноним обратиться по имени
Воскресенье, 19 Июля 2009 г. 20:23 (ссылка)
Ответить С цитатой В цитатник
Этот же символ надо в САВ поглядеть будет.


Трилистник является торическим узлом, то есть обмоткой поверхности тора — двумерного многообразия с одной дыркой.
Трилистник может быть представлен в виде двух зеркальных обличий — левого и правого, топологически не преобразуемых друг в друга, каждый из которых может быть завязан на поверхности тора без контактирующих точек скрещений, но будучи завязанными вместе на одном и том же торе, они физически контактируют друг с другом в общих точках скрещений, образуя структуру заузленной ткани на поверхности тора, представляющей собой модель точечной поверхности тора. Аналогичным образом можно построить модель точечной поверхности произвольного ориентируемого двумерного многообразия, располагая на его поверхности по меньшей мере два зеркальных узла-обмотки соответствующего типа.
Энергии упругости в заузленном стержне, зависящая от топологической сложности узла, стремясь принять наименьшее значение, приводит к тому, что его средняя линия стремится совпасть с плоскостью, в результате чего все скрещения узла становятся реально контактирующими, и их множество формирует точечную модель плоскости. При этом плоская модель точечной поверхности, заданная узлом или зацеплением нескольких узлов, в результате приложения к ней внешнего усилия и создания избыточной внутренней энергии упругости, может быть выведена из плоскости и преобразована в пространственное положение. Такие заузленные структуры, моделирующие точечные поверхностей и действующие как волновые механизмы, автор предложил называть специальным термином «NODUS структуры» (от лат. nodus, — узел).Любой узел или зацепление с некоторым количеством контактирующих скрещений, моделирует фрагмент точечной поверхности, но её обратимую кинематическую изменяемость происходящую вследствие трансформации, а не деформации структуры, могут обеспечить только те из них, которые обладают циклической упорядоченностью. Регулярность узлов и зацеплений, придающая им формообразующие свойства, проявляется в циклическом заполнении их образующими кольцевой области между двумя замкнутыми огибающими.
http://www.ronl.ru/referaty/raznoe/516444/
Трилистник может быть представлен в виде двух зеркальных обличий — левого и правого, топологически не преобразуемых друг в друга, каждый из которых может быть завязан на поверхности тора без контактирующих точек скрещений, но будучи завязанными вместе на одном и том же торе, они физически контактируют друг с другом в общих точках скрещений, образуя структуру заузленной ткани на поверхности тора, представляющей собой модель точечной поверхности тора. Аналогичным образом можно построить модель точечной поверхности произвольного ориентируемого двумерного многообразия, располагая на его поверхности по меньшей мере два зеркальных узла-обмотки соответствующего типа.
Энергии упругости в заузленном стержне, зависящая от топологической сложности узла, стремясь принять наименьшее значение, приводит к тому, что его средняя линия стремится совпасть с плоскостью, в результате чего все скрещения узла становятся реально контактирующими, и их множество формирует точечную модель плоскости. При этом плоская модель точечной поверхности, заданная узлом или зацеплением нескольких узлов, в результате приложения к ней внешнего усилия и создания избыточной внутренней энергии упругости, может быть выведена из плоскости и преобразована в пространственное положение. Такие заузленные структуры, моделирующие точечные поверхностей и действующие как волновые механизмы, автор предложил называть специальным термином «NODUS структуры» (от лат. nodus, — узел).Любой узел или зацепление с некоторым количеством контактирующих скрещений, моделирует фрагмент точечной поверхности, но её обратимую кинематическую изменяемость происходящую вследствие трансформации, а не деформации структуры, могут обеспечить только те из них, которые обладают циклической упорядоченностью. Регулярность узлов и зацеплений, придающая им формообразующие свойства, проявляется в циклическом заполнении их образующими кольцевой области между двумя замкнутыми огибающими.
http://www.ronl.ru/referaty/raznoe/516444/
https://ru.wikipedia.org/wiki/Узел_(математика)










